图像与图像增强基础

25spring BME3304 生物医学图像处理（I）的课程笔记

图像基础

常见的医学成像方式

其中除了 PET 图片有时会采用伪彩图像以外，大部分医学影像都是灰度图像. 除了常规的 PNG，JPG 等格式以外，医学影像还常用的图像格式包括 DICOM(.dcm) （本质仍是二维图像，但其包含了大量例如病人信息，设备信息等重要 metadata）以及 NIfTI(.nii/.nii.gz)（本质上是一个包含多个切片的压缩包，可在专用软件如 itksnap 等中作为一个三维模型打开）

取样与量化

• 取样：对图像坐标 $(x, y)$ 数字化
• 量化：对每个图像坐标的幅值 $f(x, y)$ 数字化

数字图像的矩阵表示

数字图像可以通过一个二维矩阵来表示, 这个矩阵的每个元素对应图像的一个像素点.

采样 (Sampling)

• 决定矩阵大小： 矩阵的尺寸由采样决定, 通常表示为 $M \times N$.
  • $M$ 和 $N$ 分别代表图像的行数和列数（即高和宽）.
• 坐标范围：
  • 水平坐标 $x$ 的范围为 $[0, M-1]$.
  • 垂直坐标 $y$ 的范围为 $[0, N-1]$.
• 矩阵中的每个元素 $f(x, y)$ 都对应一个唯一的像素点.

2. 量化 (Quantization)

• 决定灰度级数： 每个像素点的值（亮度或颜色）通过量化来确定.
  • 灰度级数 $L$ 通常是 2 的整数次幂, 表示为 $L = 2^k$, 其中 $k$ 是量化所需的位数.
• 像素值范围：
  • 矩阵中每个元素 $f(x, y)$ 的值在 $[0, L-1]$ 之间, 代表该像素点的亮度或颜色等级.

3. 存储比特数 (Storage Bits)

• 计算公式： 存储一张数字图像所需的总比特数 $b$ 为：
  • $b = M \times N \times k$
  • $M \times N$ 是总像素点数.
  • $k$ 是每个像素点所需的比特数.

数字图像的部分参数

采样相关

• DPI: dots per inch, dpi 越高越清晰

• 空间分辨率(更多用于医学图像)

  空间分辨率 = 视场 (Field of View) / 点数

  • 视场 (FOV)：指的是成像区域的物理尺寸, 即图像所覆盖的实际空间范围, 通常用毫米（mm）等长度单位表示.
  • 点数：指图像在该物理尺寸内所包含的像素点数量, 即采样得到的矩阵大小 $M \times N$ 中的M或N.

公式说明, 在视场相同的情况下, 点数越多, 空间分辨率就越高. 如果点数相同, 视场越小, 空间分辨率也越高.

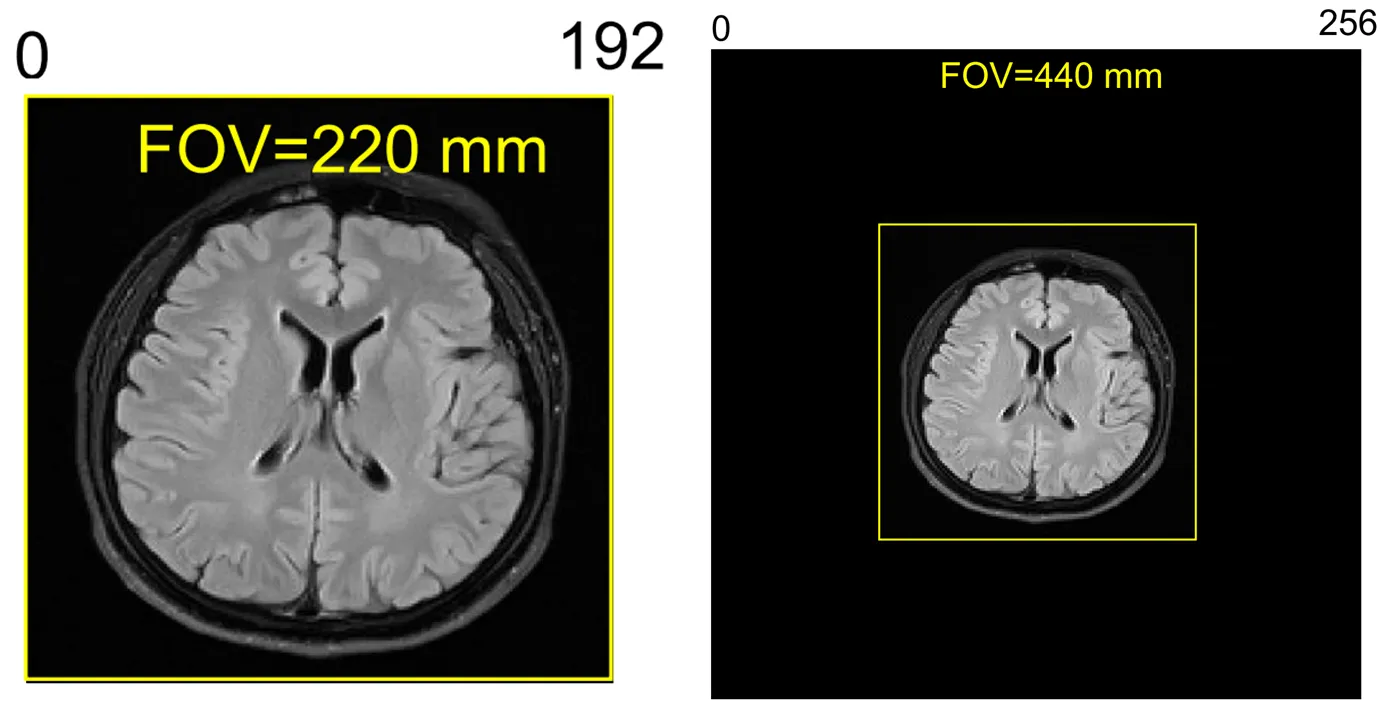
例如上图虽然右图采样点更多, 但因为 FOV 不同, 所以左侧的空间分辨率更高

量化相关

• 灰度级: 即量化精度, 灰度级 $L=2^{k}$ ，k 为量化的灰度比特
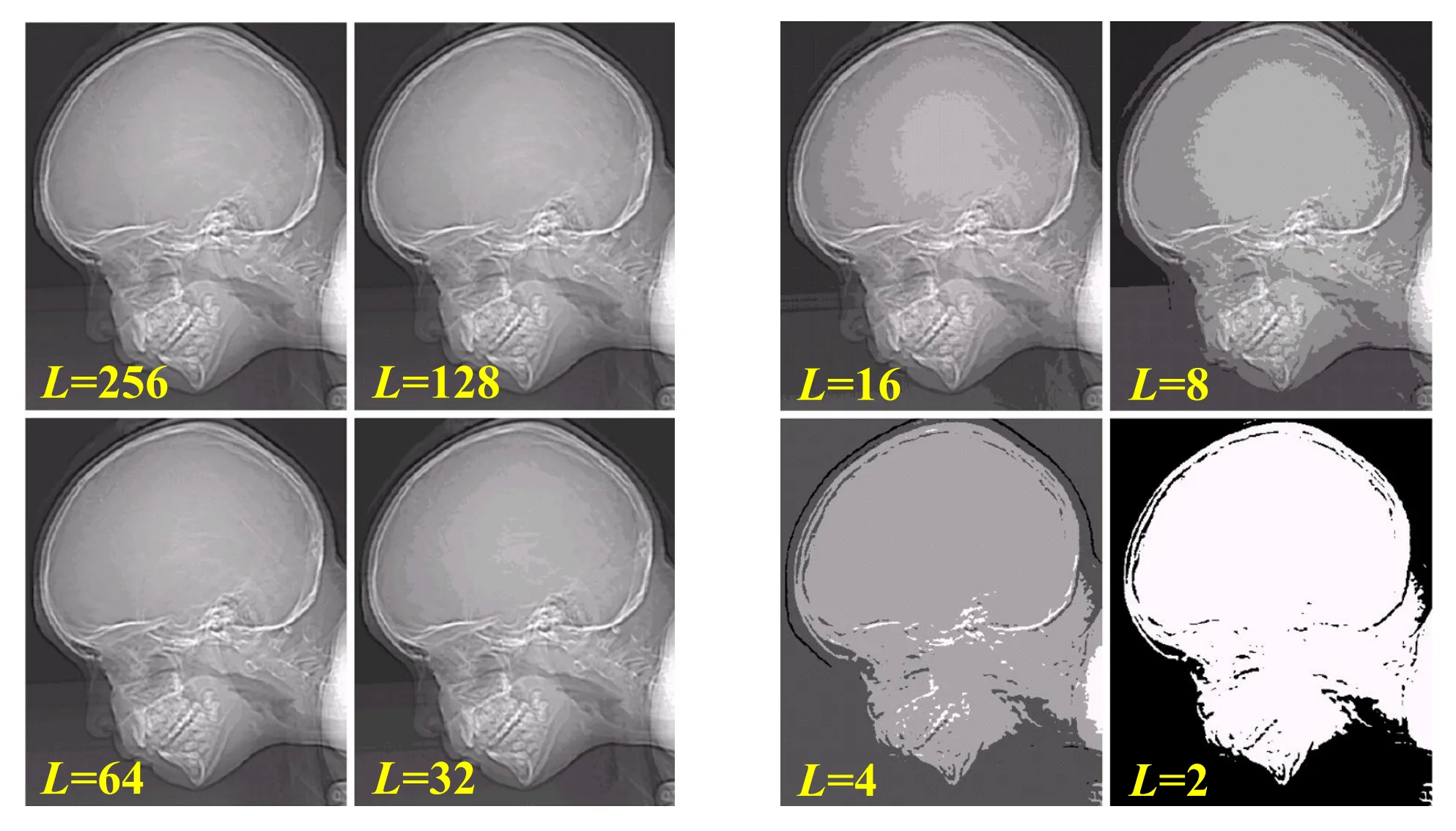
• 饱和度: 最大的灰度值, 大于此灰度的灰度固定为最大值(饱和区有固定的灰度级)
• 对比度：最高与最低灰度级之间的灰度差

图像内插

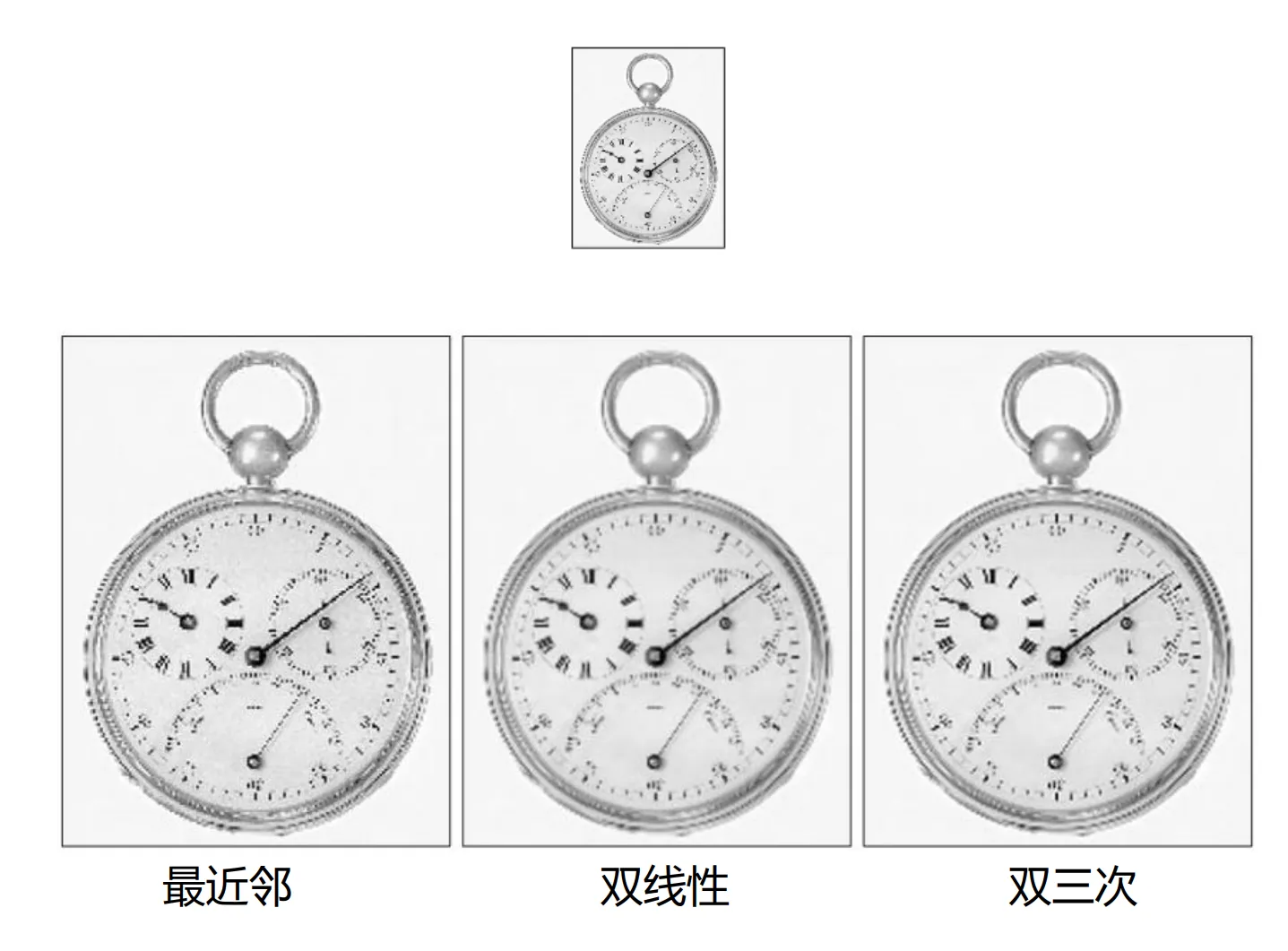
图像内插：用已知数据估计未知数据, 用于放大, 收缩, 旋转, 几何校正

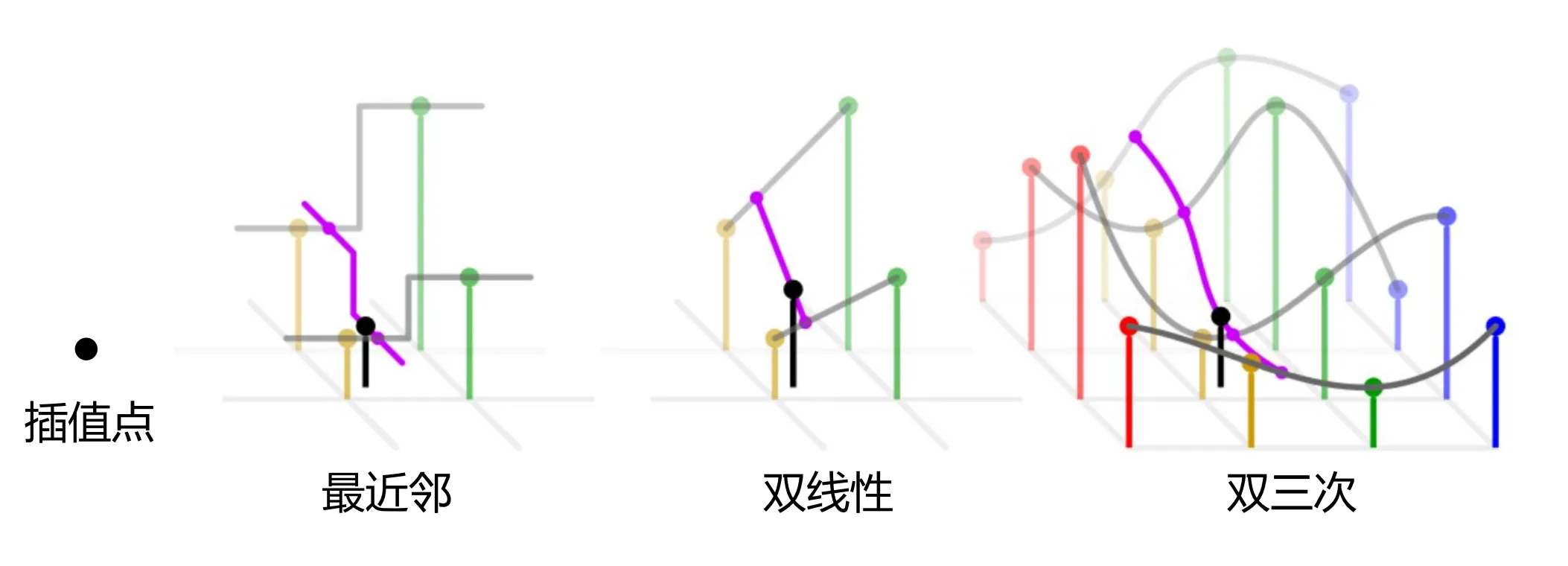
最近邻即为直接取最近已知点的灰度, 双线性其实并不是线性估计(两个线性函数相乘出现了二次项)

像素间的基本关系

相邻像素

常见的像素(指 2d)之间的领域有三种:

• 4 领域($N_4(p)$): 即与像素有边相接的边的四个像素
• 对角领域($N_D(p)$): 即与像素有顶点相接(且不共边)的四个像素
• 8 领域($N_8(p)$): 上面两个加起来 急救范围

⬛🟦⬛    🟦⬛🟦    🟦🟦🟦
🟦🟥🟦    ⬛🟥⬛    🟦🟥🟦
⬛🟦⬛    🟦⬛🟦    🟦🟦🟦
4邻域      对角邻域   8邻域

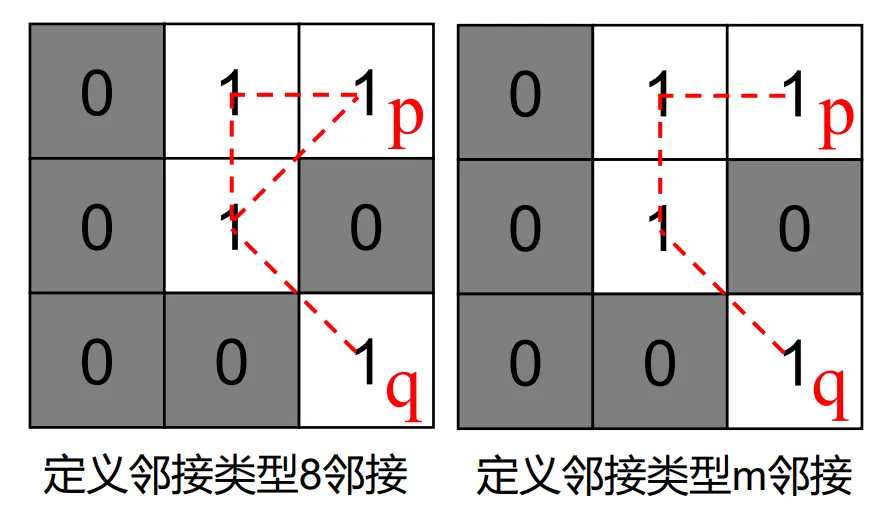
邻接性

邻接性来源与两个层面, 一个是位置意义上的邻接, 一个是灰度值上的邻接 对两点$p(x, y), q(x, y)$ 以及其灰度值 $f(p), f(q)$

• 4-邻接

  $f(p)\in V, f(q)\in V$

  $q\in N_4(p)$

  $p, q$

• 8-邻接

  $f(p)\in V, f(q)\in V=1$

  $q\in N_8(p)$

  $p, q$

• m-邻接(混合邻接)

  $f(p)\in V, f(q)\in V=1$

  $q\in N_4(p) \text{ 或 } q\in N_D(p)$

  $N_4(p)\cap N_4(q)=\emptyset$

  $p, q$

连通性

连通性必须基于邻接性, 基于不同的邻接性可能会导致连通性不同

红线走穿过的像素是 1 像素的 8 邻接, 它构成的路线就叫做通路, 也叫 8 通路.

• 同这个例子所示, 如果通路是闭合的, 就叫做闭合通路.
• 令红线穿过的像素集合为 S, 那么 S 中包含的任意两个像素 p 和 q 在 S 中是连通的.
• 对于任意一个属于集合 S 的像素 q, 集合 S 中连通到像素 q 的像素集成为 q 的连通分量. 如果 S 有一个连通分量, 则集合 S 称为连通集.

区域与边界

定义区域与边界时同样需要指定邻接性

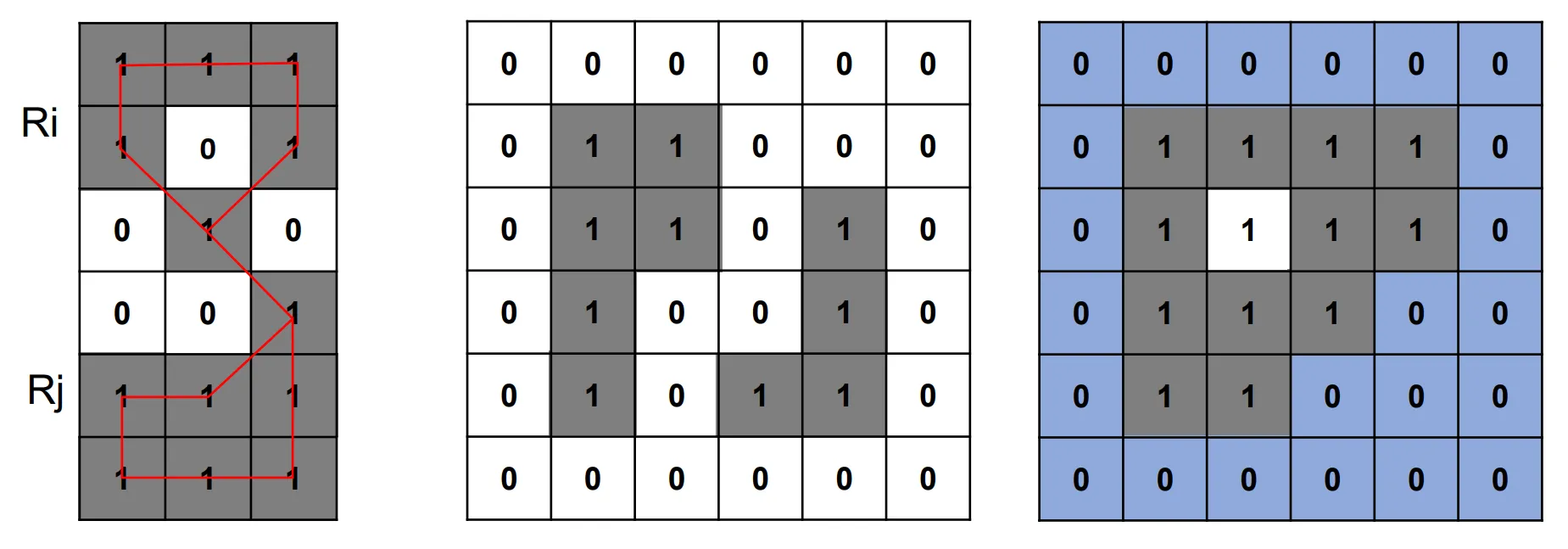
如果 R 是图像中的一个子集, 而且刚好构成连通集, 那么 $R$ 就称为一个区域.

• 区域的边界/边框/轮廓：所在区域的一个子集, 是 $R$ 中与 $R$ 的补集中像素相邻的一组像素
• 如果有两个区域 $R_i/R_j$, 可以联合（并）称为一个区域, 就称这两个区域为邻接区域.
• 假设一幅图像中有 $K$ 个不连接的区域, 且他们都不接触图像的边界, 令 $R_u$ 代表 $K$ 个区域的并 集, 并且令 $(R_u)^c$ 代表其补集. 我们称 $R_u$ 为所有点图像的前景, $(R_u)^c$ 为所有点图像的背景.

区域的部分参数 [only in BME4301]

• 周长，面积：略
• 离心率：某一点的离心率指此点到区域内任意一点的最大值
• 中心：离心率最小的点的集合
• 半径：离心率的最小值（中心到最远边界的距离）
• 直径：离心率的最大值（区域内任意两点的最长距离）
• 质心：所有像素坐标直接求算术平均
• 矩/中心矩：k，l阶中心距被定义为 $\mu_{kl} = \sum_{x} \sum_{y} (x - x_c)^k (y - y_c)^l$
• 方向 $\theta = 0.5 \arctan (\frac{2 \mu_{11}}{\mu_{20} - \mu_{02}})$

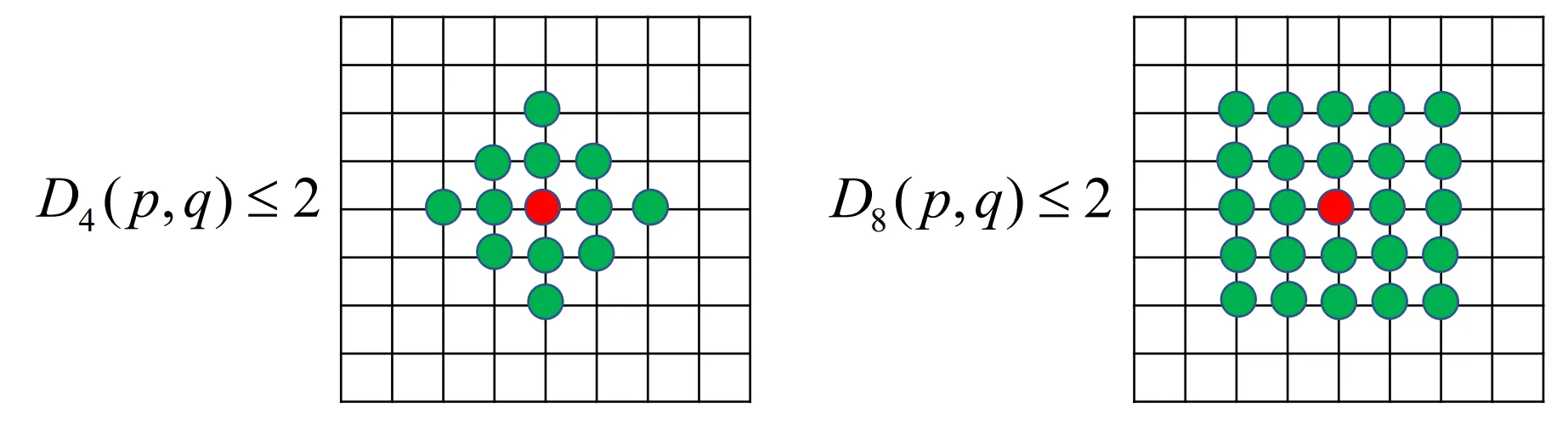
像素间的距离

• 欧氏距离 $D_e(p,q) = \sqrt{(x-s)^2 + (y-t)^2}$
• 城市街区距离 $D_4(p,q) = |x-s| + |y-t|$
• 棋盘距离 $D_8(p,q) = \max(|x-s|, |y-t|)$

阵列操作

• 图像相加: 将图像(由同一个无噪图像与随机噪声组成)相加求平均可以降低噪声
• 图像相减: 可以增强差别
• 图像乘除: 注意这里不是传统意义上的矩阵相乘, 而是逐元素乘除

图像增强

对点 $(x, y)$, 假设其灰度为 $f(x, y)$, 则经过点运算得到的新灰度值可以表示为 $g(x, y) = T[f(x, y)]$

我们称 $T$ 为点 $(x, y)$ 的某种领域上定义的算子

点运算增强

点运算结果只与像素点的灰度有关, 对像素的坐标或者像素周围的点的灰度无关, 此时增强算子可简化为 $s = T(r)$

其中, $r$ 是输入像素的灰度值, $s$ 是输出像素的灰度值. 点运算的目标就是寻找一个合适的变换 $T$.

阈值处理

阈值处理是一种简单的点运算, 可以将灰度图像转换为二值图像, 常用于提取图像轮廓.

• 函数： $$s = T(r) = \begin{cases} s_0 & \text{if } r < k \\ s_1 & \text{if } r \geq k \end{cases}$$
• 说明：当像素值 $r$ 小于阈值 $k$ 时, 赋予一个值 $s_0$（例如, 黑色）；大于或等于阈值 $k$ 时, 赋予另一个值 $s_1$（例如, 白色）.

阈值处理的计算方法

基本全局阈值迭代算法

这是一种通过循环迭代不断修正阈值，直到找到一个收敛的“中间平衡点”的方法。这种方法假设一个理想的阈值应该位于背景像素平均灰度和目标像素平均灰度的中间。算法通过不断更新阈值来逼近这个位置。

1. 初始化： 选择一个初始阈值 $T_0$（通常取整幅图像的平均灰度值）。
2. 分割： 用当前的 $T$ 将图像分割成两组像素：
   • $G_1$：灰度值 $> T$ 的像素（前景/亮部）
   • $G_2$：灰度值 $\le T$ 的像素（背景/暗部）
3. 计算均值： 分别计算 $G_1$ 和 $G_2$ 区域内像素的平均灰度值 $\mu_1$ 和 $\mu_2$。
4. 更新阈值： 计算新的阈值：$T_{new} = \frac{1}{2}(\mu_1 + \mu_2)$。
5. 迭代判断： 计算新旧阈值的差值 $\Delta T$。
   • 如果 $\Delta T < \epsilon$（预设的收敛参数，如 0），则停止，输出当前 $T$。
   • 否则，令 $T = T_{new}$，返回第 2 步继续循环。

这种算法的好处是逻辑与实现都非常直观，但其计算量较大，对复杂图片可能迭代轮次较多。

Otsu 算法（大津法）

被认为是全局阈值处理中最佳的方法之一。它不需要迭代，而是基于统计学原理寻找“最佳”分割点。这种算法在思想上仍然认为好的图像分割应该满足两个条件：区域内相似性/方差最高，区域间相似性/方差最低。即找到能使 $\sigma_B^2 = \omega_0 \omega_1 (\mu_0 - \mu_1)^2$ 或者 $\sigma_b^2(t) = \omega_0(\mu_0 - \mu_T)^2 + \omega_1(\mu_1 - \mu_T)^2$ 最大的阈值。而由于 $\sigma_T^2 = \sigma_w^2 + \sigma_b^2$ （反正可以证），因此最大化类间方差 $\sigma_B^2$ 等价于最小化类内方差 $\sigma_w^2$。

Otsu 法的代码实现：

def otsu_threshold(image_path: str) -> int:
    image: Image.Image = Image.open(image_path).convert("L")
    image_array: np.ndarray = np.array(image)

    hist, _ = np.histogram(image_array.flatten(), bins=256, range=(0, 255))
    hist_norm: np.ndarray = hist / hist.sum()

    cum_sum: np.ndarray = np.cumsum(hist_norm)
    cum_mean: np.ndarray = np.cumsum(hist_norm * np.arange(256))

    global_mean: float = cum_mean[-1]

    valid_mask: np.ndarray = (cum_sum > 0) & (cum_sum < 1)
    variances: np.ndarray = np.zeros(256)

    variances[valid_mask] = (
        global_mean * cum_sum[valid_mask] - cum_mean[valid_mask]
    ) ** 2 / (cum_sum[valid_mask] * (1 - cum_sum[valid_mask]))

    threshold: int = int(np.argmax(variances))
    return threshold

这里面倒数第二行的 variances 数组是上文提到的类间方差的一种化简形式，我们知道原始的类间方差 $\sigma_b^2 = \omega_0 (\mu_0 - \mu_t)^2 + \omega_1 (\mu_1 - \mu_t)^2$ , 而我们知道累计均值函数（也就是 cum_mean 数组）可以表示为 $m(t) = \mu_t \cdot \omega(t)$ 的形式，且 $\mu_{global} = \omega_0 \mu_0 + \omega_1 \mu_1$ 。因此我们可以得到 $\mu_0 = \frac{m(t)}{\omega_0}, \mu_1 = \frac{\mu_{global} - \mu_0}{\omega_1}$

回代到原始公式有

其中 $\mu_{global}(1 - \omega_1) - m(t) = \omega_0\mu_{global} - m(t)$ 即得到

转换成代码也就是上述的实现。

Otsu 算法对噪声较为敏感，因此对噪声较高的图像可以先进行平滑处理再使用 Otsu 算法。除此之外，Otsu 算法对目标占比非常小（即直方图中只有一个峰值明显高于其他峰值）的图像分割效果不佳。

Otsu 同样可以设置多阈值版本，不过计算量会随阈值数量上升而上升。

最大熵（Entropy）[only in BME4301]

比 Otsu 算法好理解一点，假设阈值为 t，最大熵的目标阈值就是找到合适的 t 使

最大。代码实现比较简单就不贴了。

其他阈值算法 [only in BME4301]

• 三角算法：感觉看图比较直观，即找到最大化 d 的阈值

• 自适应阈值：不同区域采用不同的阈值。

图像反转

图像反转用于增强嵌入在图像暗区域中的白色或灰色细节. 它将亮的像素变暗, 暗的像素变亮.

• 函数： $s = T(r) = L - 1 - r$
• 说明：$L$ 是图像的灰度级数（例如, 对于 8-bit 图像, $L=256$）. 此变换将黑变成白, 白变成黑.

对数变换

对数变换主要用于图像灰度级的扩展和压缩, 特别适合处理傅里叶频谱等动态范围非常大的图像.

• 函数： $s = T(r) = c \cdot \log(1 + r)$
• 特点：
  • 扩展低灰度区：将输入图像中较窄的低灰度值区域映射到输出图像中一个更宽的范围.
  • 压缩高灰度区：将输入图像中较宽的高灰度值区域映射到输出图像中一个更窄的范围.
  • 常数 $c$ 用于控制输出灰度值的范围.

左: 阈值处理, 中: 图像反转, 右: 对数变换

幂律 (伽马) 变换

幂律变换是一种应用广泛的技术, 通过调整参数 $\gamma$ (gamma) 可以灵活地改变图像的对比度.

• 函数： $s = T(r) = c \cdot r^\gamma$
• 特点：
  • $\gamma < 1$：提升暗部细节, 使图像整体变亮（扩展暗色灰度级）.
  • $\gamma > 1$：提升亮部细节, 使图像整体变暗（压缩暗色灰度级）.
• 应用：广泛用于校正显示器等设备的非线性响应（伽马校正）. 例如, 显示器的灰度-电压响应通常 $\gamma$ 值在 $1.8$ 到 $2.5$ 之间.

幂律变换可以被理解为可定制程度更高的对数变换, 二者都能实现压缩一部分灰度级, 扩展一部分灰度级.

分段线性变换

与上述平滑的非线性函数不同, 分段线性变换提供了更强的灵活性, 允许用户根据需要定义更复杂的变换, 对策性较高(上限高, 理论可以实现任意变换), 泛用性较差(需要自定义的参数较多)

对比度拉伸

通过拉伸特定灰度范围来提高图像的动态范围, 从而增强图像对比度. 变换函数通常由几个关键点 $(r_1, s_1)$ 和 $(r_2, s_2)$ 定义的折线构成, 本质仍然是扩展部分灰度级, 压缩部分灰度级

灰度级分层

用于突出图像中特定的灰度范围, 有两种主要方式：

1. 突出目标范围, 消除其他：将目标范围 $[A, B]$ 内的像素值设为一个固定较高的值, 而将范围外的像素值设为一个固定较低的值.
2. 突出目标范围, 保留其他：将目标范围 $[A, B]$ 内的像素值设为一个固定的值, 同时保持其他区域的灰度值不变.

比特平面分层

像素值是由比特组成的数字, 每个比特位代表了图像的不同信息. 将图像分解成各个比特平面（例如, 对于 8-bit 图像, 可以分解为 8 个 1-bit 的比特平面）可以帮助分析每个比特位对图像整体的贡献.

• 高阶比特平面（如第 7, 8 位）包含了图像大部分的视觉信息.
• 低阶比特平面（如第 1, 2 位）则包含了更多的细节和噪声信息.

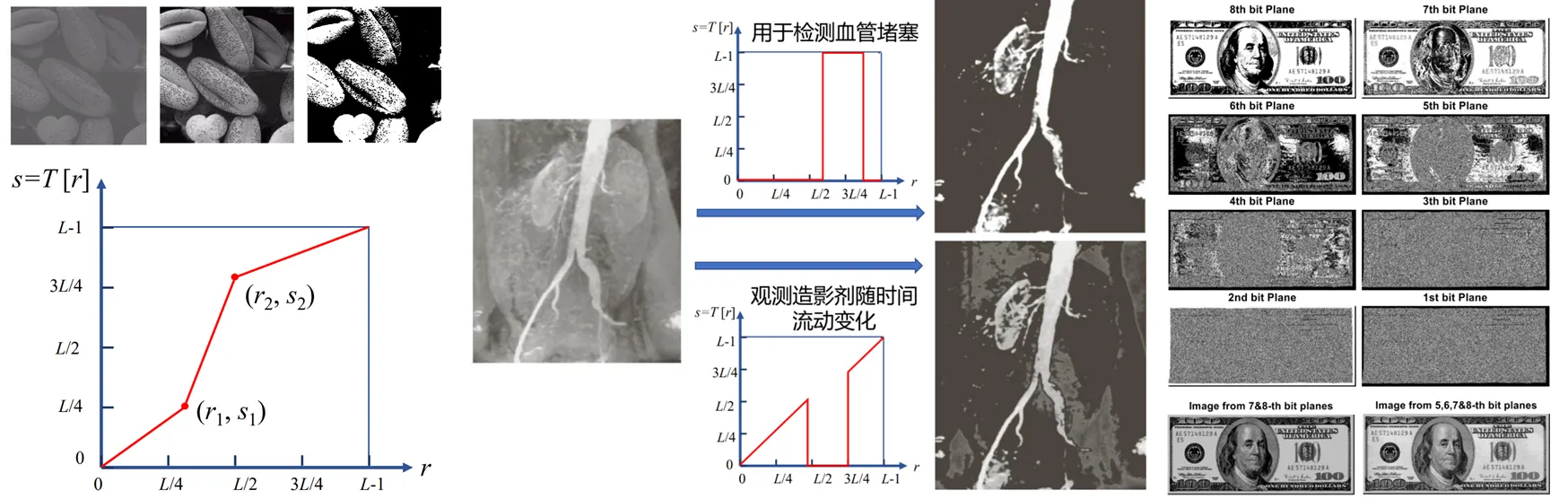
左: 对比度拉伸, 中: 灰度级分层, 右: 比特平面分层

直方图均衡化

灰度直方图

灰度直方图是图像中灰度级分布的图形化表示, 它统计了每个灰度级所拥有的像素数量.

函数表示： $h(r_k) = n_k$

$r_k$：第 $k$ 阶灰度级 (例如 $0, 1, ..., L-1$).

$n_k$：图像中灰度值为 $r_k$ 的像素总数.

核心思想：直方图反映了图像灰度值的分布情况, 但失去了像素的空间位置信息. 不同的图像可能拥有相同的直方图.

为了进行数学分析, 通常将直方图归一化.

概率密度函数 (PDF - Probability Density Function)：表示图像中某个灰度级出现的概率.

$P_r(r_k) = \frac{n_k}{MN}$

其中 $MN$ 是图像的总像素数. 所有灰度级的概率之和为 $1$.

累积分布函数 (CDF - Cumulative Distribution Function)：表示从灰度级 $0$ 到某个灰度级 $r_k$ 出现的概率之和.

$F_r(r_k) = \sum_{i=0}^{k} P_r(r_i)$

直方图均衡化原理

直方图均衡化的核心目标是找到一个灰度变换函数 $s = T(r)$, 使得处理后图像的直方图尽可能地平直（均匀分布）.

视觉效果：一个均匀分布的直方图通常对应于一幅具有高对比度, 灰度层次丰富的图像, 因为像素值充分利用了整个灰度范围.

为了使变换后的灰度级 $s$ 均匀分布, 其概率密度函数应为一个常数： $P_s(s) = \frac{1}{L-1}$.

通过概率论可以证明, 满足这一条件的变换函数正是原始图像灰度级的累积分布函数 (CDF).

连续形式：

$s = T(r) = (L-1) \int_0^r P_r(w)dw$

离散形式：在数字图像处理中, 我们使用求和代替积分.

$s_k = T(r_k) = (L-1) \sum_{j=0}^{k} P_r(r_j) = (L-1) \cdot \text{CDF}(r_k)$

这个公式是直方图均衡化的核心计算步骤. 它将输入灰度级 $r_k$ 映射到一个新的输出灰度级 $s_k$.

计算输入图像的灰度直方图 ($n_k$).

计算每个灰度级的概率 ($P_r(r_k)$).

计算灰度级的累积分布 ($CDF(r_k)$).

应用变换公式 $s_k = (L-1) \cdot \text{CDF}(r_k)$, 并将结果取整, 得到新的灰度映射关系.

使用这个映射关系替换原图像中每个像素的灰度值.

注意：由于像素灰度值是离散的且需要取整, 最终得到的直方图并不会绝对平坦, 但会趋向于均匀分布.

直方图规定化

直方图均衡化的好处在于它能自动调整图像的对比度, 但自动的也不一定是最好的, 有时我们希望图像的直方图符合某种特定的分布, 这时就需要使用直方图规定化（也称为直方图匹配）.

直方图规定化（也称直方图匹配）是一种交互式的图像增强技术. 它的核心目标是修改一幅图像的直方图, 使其形状匹配一个预先规定的目标直方图.

直方图的规定化和标准化其实从原理上是比较相似的, 二者都是通过更改灰度映射来使原灰度直方图更改为一个新的分布函数, 只是标准化是将直方图变为均匀分布 即 $p_{s} \equiv \frac{1}{L-1}$ , 而规定化可以变为任意分布函数.

变化步骤

1. 对原始图像进行直方图均衡化, 得到一个变换 $s = T(r)$. 处理后的图像直方图理论上是均匀的.
2. 对目标直方图进行直方图均衡化, 得到另一个变换 $v = G(z)$. 处理后的直方图理论上也是均匀的.
3. 因为 $s$ 和 $v$ 都来自均匀分布, 我们可以认为它们是等价的, 即 $s = v$.
4. 因此, 我们得到关系式：$T(r) = G(z)$.
5. 为了找到原始灰度 $r$ 对应到哪个目标灰度 $z$, 我们需要求解 $z$, 即找到 $G$ 的反函数 $G^{-1}$. $$z = G^{-1}(s) = G^{-1}(T(r))$$

这个公式 $z = G^{-1}(T(r))$ 构成了直方图规定化的理论核心. 它表明, 要将原始灰度 $r$ 映射到目标灰度 $z$, 需要先对 $r$ 进行均衡化得到 $s$, 然后找到一个灰度值 $z$, 这个 $z$ 在经过其自身的均衡化变换 $G$ 后, 结果恰好等于 $s$.

空间滤波

回到我们对图像处理的定义 $g(x, y) = T[f(x, y)]$, 我们知道, 当 $T$ 的定义域 1*1 时, 就是点运算增强, 当其定义域是在某个邻域的(m*n)时, 就是空间滤波. 空间滤波的机制时其输出图像的每一点都是输入图像中某一个区域的映射, 本质是一种相关/卷积运算. 空间滤波器又称为掩膜/窗口, 其模板的形式没必要时矩形, 不过矩形在数学上易于描述, 也易于实现.

空间滤波可以分为相关运算和卷积运算, 卷积运算就是直接把滤波器与对应窗口上的像素直接进行逐元素相乘再相加, 而卷积运算则是先将滤波器进行 180 度旋转(中心翻转)再进行相关运算. 不过也很容易通过定义看出来, 只要是中心对称的滤波器, 那么相关和卷积是等价的, 所以这两种在大部分应用中其实都是等价的, 只有滤波器是非对称的(比如 Sobel 算子等)才会有区别.

边界处理

在进行空间滤波时, 边界处理是一个重要的问题. 由于滤波器通常是一个局部窗口, 当窗口位于图像边缘时, 可能会出现一些像素没有足够的邻域信息可供计算. 这就需要对边界进行处理, 以确保滤波操作的有效性, 这种边界处理一般分为三类: 直接忽略边界部分, 或者把边界外再用 0 或者边界像素值填充. 至于用边界像素值填充时, 又可以分为复制(replicate)边界像素值, 反射(symmetric)边界像素值, 循环(circular)边界像素值等方式.

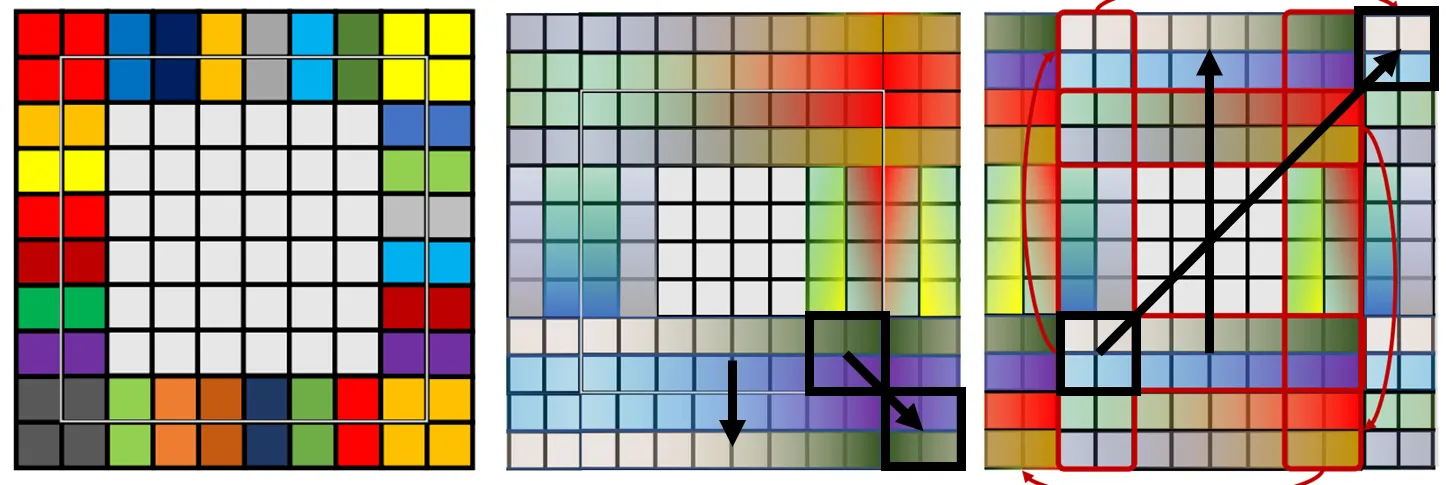
从左至右: 复制, 反射, 循环

平滑滤波器

平滑滤波器通过削弱图像的高频成分突出低频成分来达到滤除噪声, 模糊图像的目的.

常见的噪声种类包括高斯噪声, 泊松噪声, 乘性噪声, 椒盐噪声等.

平滑线性滤波器即是用滤波器模板领域内的像素的(加权)平均值去代替每个像素点的平均值, 又名均值滤波器, 是低通滤波器的一种, 常见模板:

• 3*3 均值模板:$\frac{1}{9} * \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix}$

• 4 邻域均值模板:$\frac{1}{5} * \begin{bmatrix} 0 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 0 \end{bmatrix}$

• 加权平均模板:$\frac{1}{10} * \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 1 \end{bmatrix}$

• 3*3 高斯模板: $\frac{1}{16} * \begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{bmatrix}$

在这里加一分母是为了防止加起来超出灰度范围, 特别地, 如果所有系数都相等的滤波器也叫做盒状滤波器

统计排序滤波器

统计排序滤波器通过对滤波器领域内的像素值进行排序来确定输出像素值, 常见的有中值滤波器, 最大值滤波器和最小值滤波器, 也就是把领域内的像素值排序后取中间值, 最大值, 最小值作为输出像素值. 中值滤波是另一种消除噪声的办法, 同时也可以避免边缘模糊, 最大值滤波器则可以用于寻找图像中的亮点或者腐蚀亮区相邻的暗域, 而最小值滤波器则可以用于寻找图像中的暗点或者腐蚀暗区相邻的亮域.

不过, 中值滤波器是一种非线性滤波器, 其不可避免地会改变图像的一些性质, 所以对于某些场合(比如部分医学图像处理)是不太能接受的.

锐化滤波-拉普拉斯增强

如果把图像平滑的求和平均视为一种类似积分的运算, 那么图像锐化就是一种类似微分运算(梯度运算), 其可以加强高频, 弱化低频, 以增强细节和边缘, 达到去模糊的作用.

梯度运算通过计算图像灰度的“微分”来检测边缘和细节, 是图像锐化的核心思想. 图像平滑可以看作是“积分”运算, 而锐化则对应“微分”运算.

一阶微分 (First-Order Derivative) 用于检测图像中灰度变化的起始点, 常用于边缘检测.

$\frac{\partial f}{\partial x} = f(x+1) - f(x)$

一阶微分对灰度阶梯响应强：在图像灰度值发生跳变（边缘）的地方, 一阶微分会产生一个峰值, 对缓坡响应恒定：在灰度值缓慢, 线性变化的区域（斜坡）, 一阶微分的响应是一个常量. 对平坦区域响应为零：在灰度值没有变化的区域, 一阶微分结果为 0. 但产生较宽的边缘：由于它在整个斜坡区域都有响应, 因此检测到的边缘通常比较粗.

而二阶微分 (Second-Order Derivative) 检测的是灰度变化的“变化率”, 对图像中的精细细节更敏感.

$\frac{\partial^2 f}{\partial x^2} = [f(x+1) - f(x)] - [f(x) - f(x-1)] = f(x+1) + f(x-1) - 2f(x)$ 二阶微分对细节响应强：对图像中的细线和孤立点响应非常强烈, 其会对灰度阶梯产生双响应：在灰度阶梯的开始和结束处各产生一个响应（一正一负）, 并在两者之间形成零交叉 (Zero-Crossing). 这使得边缘定位更精确. 而对缓坡响应为零：在灰度值线性变化的区域, 二阶微分的响应为 0/

在大多数一般图像增强应用中, 二阶微分的效果比一阶微分更好, 因为它形成细节的能力更强, 而一阶微分由于其产生粗边缘的特性, 主要用于提取和分割图像中的边缘轮廓.

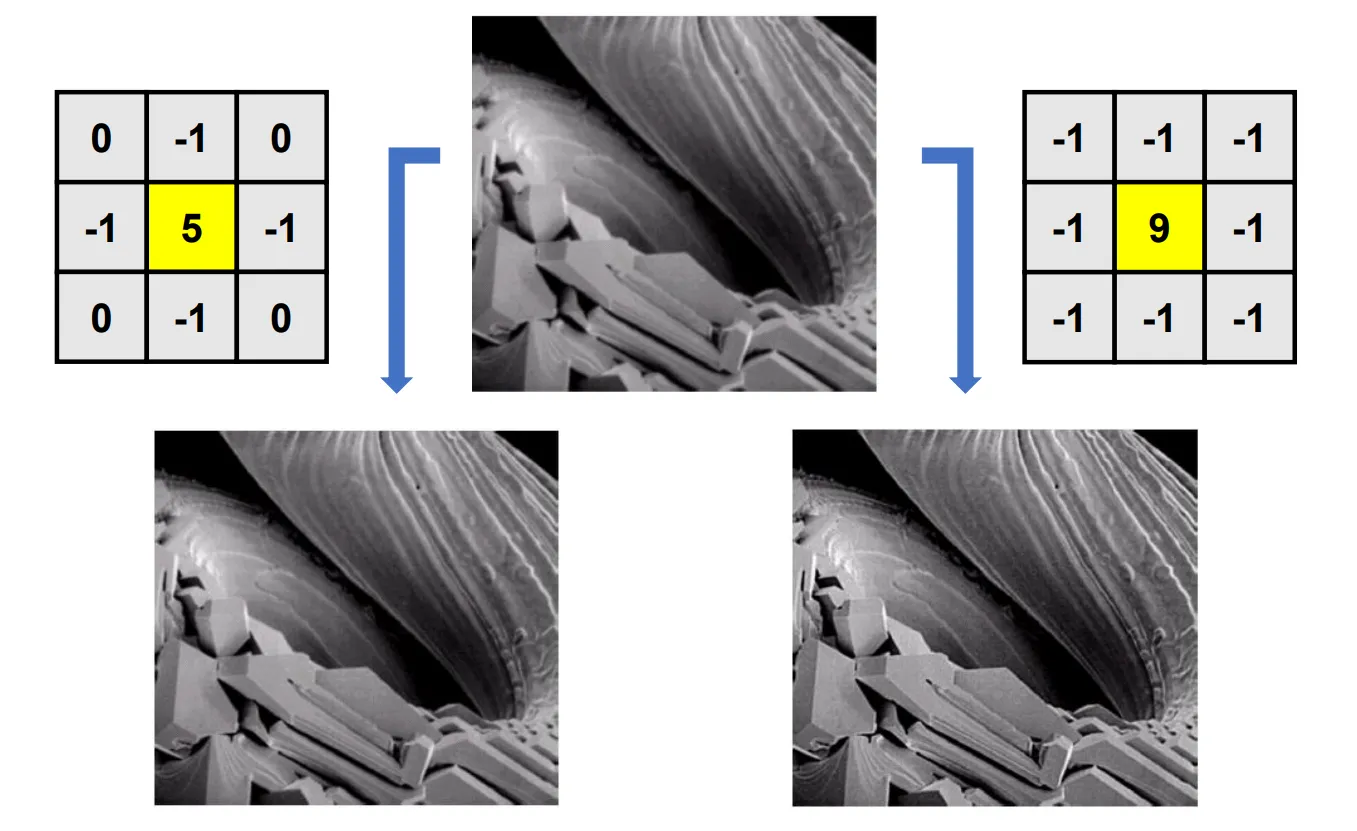
常见的拉普拉斯算子: $\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}, \begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{bmatrix}, \begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{bmatrix}, \begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{bmatrix}$

锐化滤波器通常通过将原始图像与其拉普拉斯变换的结果相加来实现: 如果拉普拉斯掩膜中心系数为负则相减, 若中心为正则相加.

不过, 锐化滤波器由于存在相减运算, 所以其可能出现负数灰度值, 我们可以把所有负值都用 0 代替, 不过这样会导致图片中黑色区域较多; 或者我们可以把所有像素全部加上最小值的绝对值, 即整体抬到到最小值为 0.

当然拉普拉斯算子不一定需要所有系数之和为 0, 也可以通过增大中心系数(的绝对值)来增强锐化效果.

锐化滤波-非锐化/钝化掩蔽

也就是先平滑后锐化, 其本质上是一种边缘增强技术, 通过从原始图像中减去平滑图像来提取图像的高频成分（边缘和细节）, 然后将这些高频成分添加回原始图像以增强边缘.

锐化滤波-梯度增强

• 梯度算子 (Gradient Operator) $\nabla f = \begin{bmatrix} g_x \\ g_y \end{bmatrix} = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}$ 线性算子, 非各项同性

• 梯度模量 (Gradient Magnitude) $M(x, y) = \text{mag}(\nabla f) = [g_x^2 + g_y^2]^{1/2}$ 非线性算子, 各项同性

由于平方根运算比较耗时, 通常我们对梯度模量进行近似求解, 不同近似方法可以得到不同的近似梯度算子.

• 基本梯度算子

  $$g_x = f(x+1, y) - f(x, y) \\ g_y = f(x, y+1) - f(x, y)$$

  对应模板:

  $$g_x: \begin{bmatrix} 1 & -1 \\ 0 & 0 \end{bmatrix}, \quad g_y: \begin{bmatrix} 1 & 0 \\ -1 & 0 \end{bmatrix}$$

• 交叉梯度算子(Roberts 算子)

  $$g_x = f(x, y) - f(x+1, y+1) \\ g_y = f(x+1, y) - f(x, y+1)$$

  对应模板:

  $$g_x: \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}, \quad g_y: \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$$

  Roberts 算子特点是边缘定位准, 但是对噪声比较敏感

• Sobel 梯度算子

  $$g_x = [f(x+1, y-1) + 2f(x+1, y) + f(x+1, y+1)] - [f(x-1, y-1) + 2f(x-1, y) + f(x-1, y+1)] \\ g_y = [f(x-1, y+1) + 2f(x, y+1) + f(x+1, y+1)] - [f(x-1, y-1) + 2f(x, y-1) + f(x+1, y-1)]$$

  对应模板:

  $$g_x: \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}, \quad g_y: \begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{bmatrix}$$

  相对 Roberts, Sobel 算子减小了噪声的影响, 因此在实际应用中更为常用.