近代图像处理先锋技术科普

25spring BME4301 计算机辅助手术与治疗技术的课程笔记

测地线与分水岭

测地距离 (Geodesic Distance)

设 $F_a$ 为一个连通区域。在 $F_a$ 中，两个像素 $x$ 与 $y$ 之间的测地距离 $d_{F_a}(x, y)$ 是连接 $x$ 和 $y$ 且完全包含在 $F_a$ 内的路径 $P$ 长度的下确界：

$d_{F_a}(x, y) = \wedge \{l(P)\}$

其中，“ $\wedge$ ” 代表下确界（infimum），而 $l(P)$ 是路径 $P$ 的长度。

测地线影响区与影响区骨架

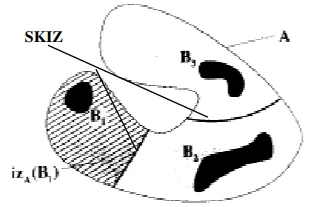
首先我们假设通过之前提到的例如 Ultimate Erosion，或者什么别的办法或者自己手动选取了若干个种子点 $S = \{s_1, s_2, ..., s_n\}$ ，那么对于图像中任意一个像素 $x$ ，我们可以计算其到各个种子点的测地距离 $d_{F_a}(x, s_i)$ ，然后我们可以将 $x$ 分配给距离其最近的种子点 $s_k$ ，每个种子点所获得的像素组合在一起就形成了对应的测地线影响区（Geodesic Influence Zone, IZ）。而那些距离两个或多个种子点距离相等的像素点就形成了影响区骨架（Influence Zone Skeleton, IZS）。

假设区域 $A$ 包含一个集合 $B$ ，该集合由若干连通分量 $B_1, B_2, \dots, B_k$ 组成。 $IZ$ 记作 $iz_A(B_i)$ ，其定义如下：

$iz_A(B_i) = \{p \in A, \forall j \in [1, k] / \{i\}, d_A(p, B_i) < d_A(p, B_j)\}$

而在区域 $A$ 中，不属于任何测地影响区 (IZ) 的点构成了集合 $B$ 在 $A$ 内部的 SKIZ，记作 $SKIZ_A(B)$ ：

$SKIZ_A(B) = A \setminus IZ_A(B)$ $\text{其中，} IZ_A(B) = \bigcup_{i \in [1, k]} iz_A(B_i)$

$A \setminus B$ 表示 $A$ 中除去属于 $B$ 的成员外的所有成员（且 $B \subset A$ ）。

👆数学定义晕晕看不懂？🤓 也没关系，因为其实窝也没看直接从ppt里面贴出来的。

分水岭变换 (Watershed Transform)

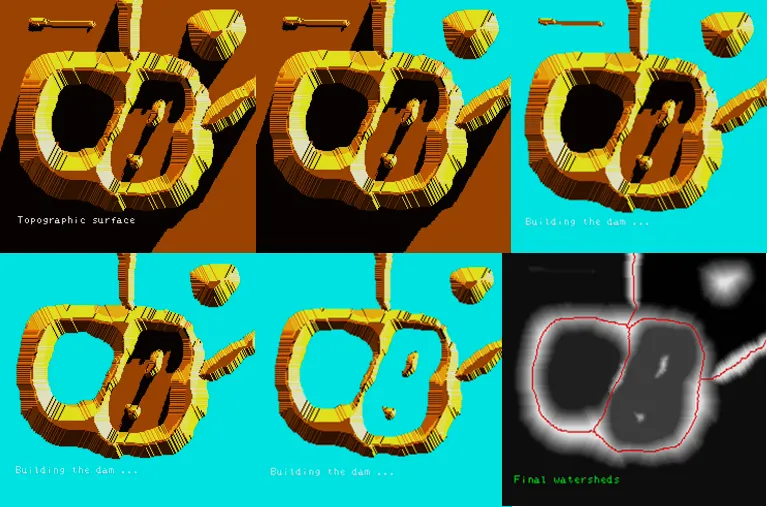
一种基于测地线相关理论的分割方法，在上文我们研究灰度级形态学时，为了便于理解，我们将二维图片放到了三维空间里，每个像素的灰度值就代表其在 z 轴上的高度，在分水岭算法里我们同样可以将整幅图像看作一个地形图，那么图像中的低灰度值区域就相当于地形图中的低洼区域，而高灰度值区域就相当于高地。假设我们从低灰度值区域开始注水，那么水会逐渐填满这些低洼区域，当水位上升到一定程度时，不同低洼区域的水会开始汇合，这时我们可以在这些汇合处建立堤坝来阻止水的流动，最终当整个地形图都被水淹没时，这些堤坝就形成了分割线，这些分割线就是分水岭。

更严谨的分步描述：

将图片中的所有像素按其灰度值排序
选取灰度最小的所有像素点作为种子点
灰度值++，选择当前灰度值的所有像素，如果这些灰度值像素是局部最小值，则加入种子点序列，如果不是，则计算器所属的测地线影响区和整张图片的SKIZ
重复3，直到所有像素都被处理完毕

注：每次计算测地线影响区都是只计算新增的这部分所属的测地线影响区和SKIZ，换言之，每个像素所属的测地线影响区所属的中心种子点一定是小于等于像素灰度值的。

Watershed 的改进

markered watershed：

手动添加数个marker，这些marker会被强制作为种子点，且在处理过程中不会加入新的种子点。这是相比起直接求影响区骨架，这种办法考虑了灰度的存在。使分割得到的分界线更合理
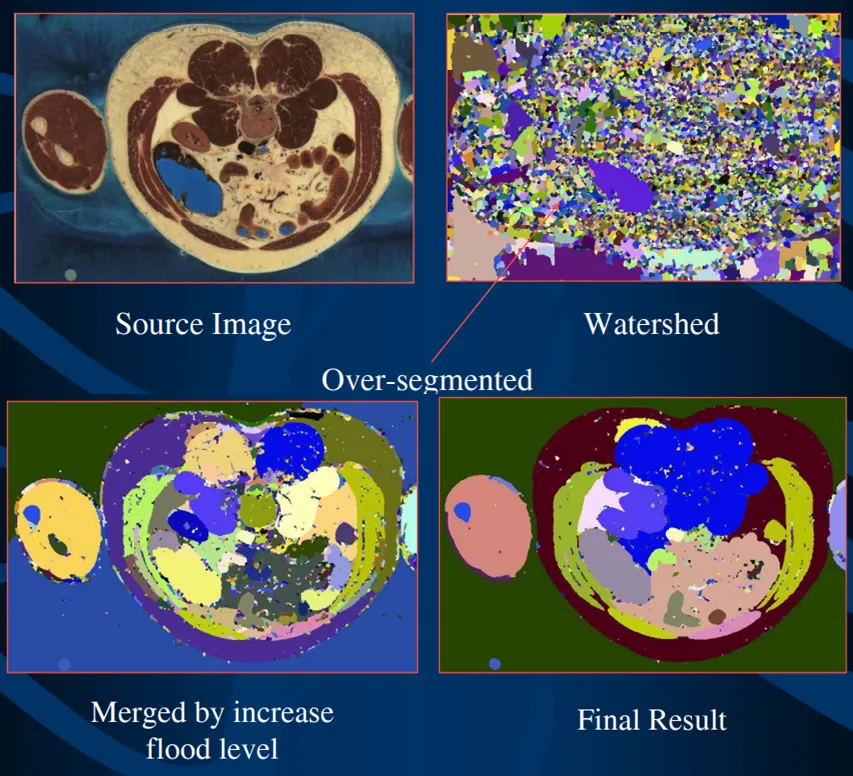
防止过分割：

在结束分水岭后，如果发现分割得到的结果极其稀碎，可以对相邻且灰度差较小的部分进行合并。

图像处理工具库

VTK (Visualization Toolkit)

使用C++编写的开源跨平台图形处理库，也包含python等语言的接口。一方面，其提供了对OpenGL或者一些底层图形api的高阶封装，能更简洁地实现医学影像中所需要的渲染3d图像的功能。另一方面，其也提供了大量的图像处理算法实现，可以直接调用。除此之外，其也拥有诸多交互式与可视化工具，使其能轻易与Qt等图形界面开发工具对接。

ITK (Insight Segmentation and Registration Toolkit)

ITK同样是用来处理医学影像的开源跨平台图像处理库，更为激进地利用了modern cpp的诸多特性，因此其实现的算法性能优于VTK，可开发性与拓展性也更高，但由于并不包含VTK含有等的如可视化等功能。一般也是和VTK配合着使用。

彩色图像与3D图像

彩色图像

彩色图像的表示方法

最常见的两种彩色图像的表示方法即为RGB和HSI。

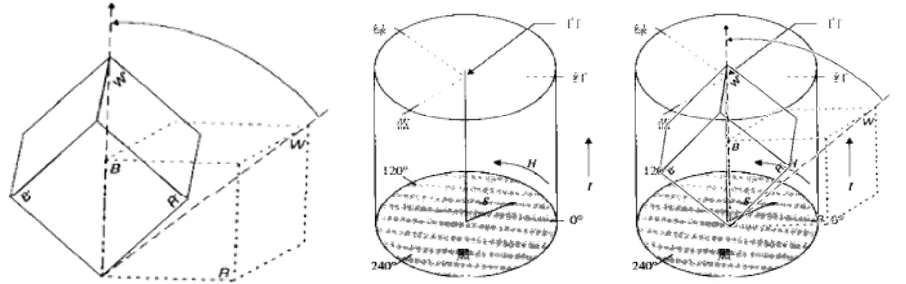
RGB将颜色放在三维直角坐标系中表示，则所有颜色向量都可以放在一个立方体里面，立方体共8个顶点，与坐标系原点重合的即为黑色（0，0，0）与原点对角的点即为白色（255，255，255）而落在每个坐标轴上的即为三原色（红，绿，蓝）与对角点相接的三个顶点表示的三个次原色：黄（255，255，0）紫/品红（255，0，255）青（0，255，255）

HIS则将颜色表示在柱坐标系中，z轴即为亮度（即底部圆心为黑色，顶部圆心为白色）而色度（Hue）则表示为绕z轴旋转的角度，饱和度（Saturation）则表示为从z轴向外的距离。

二者可以互相转换，直观地理解，转换方式是将RGB立方向上翻转，使原点（表示黑色的点）与柱坐标系底部圆心重合，白色点（对角点）与柱坐标系顶部圆心重合，红色轴（x轴）与极坐标系的0度方向重合，然后根据点在立方体中的位置即可得到其在柱坐标系中的位置，反之亦然。

但是实际的转换公式挺地狱的，可能三年前我还是高中生的时候还会推，但现在推也推不出来背也背不住还是希望老师别考了吧。

RGB -> HSI：
$S = \frac{\rho}{\rho_{\max}} = 1 - \frac{3 \min(R, G, B)}{R + G + B} = 1 - \frac{\sqrt{3}}{I} \min(R, G, B) \\ \theta = \cos^{-1} \left[ \frac{\frac{1}{2}[(R - G)] + (R - B)}{\sqrt{(R - G)^2 + (R - B)(G - B)}} \right] \\ H = \begin{cases} \theta & G \ge B \\ 2\pi - \theta & G \le B \end{cases}$
HSI -> RGB：

\begin{aligned} & 0^{\circ} \le H < 120^{\circ} \\ & R = \frac{1}{\sqrt{3}} \left[ 1 + \frac{S \cos(H)}{\cos(60^{\circ} - H)} \right] \quad B = \frac{1}{\sqrt{3}}(1 - S) \quad G = \sqrt{3}I - R - B \\ \\ & 120^{\circ} \le H < 240^{\circ} \\ & G = \frac{1}{\sqrt{3}} \left[ 1 + \frac{S \cos(H - 120^{\circ})}{\cos(180^{\circ} - H)} \right] \quad R = \frac{1}{\sqrt{3}}(1 - S) \quad B = \sqrt{3}I - R - G \\ \\ & 240^{\circ} \le H < 360^{\circ} \\ & B = \frac{1}{\sqrt{3}} \left[ 1 + \frac{S \cos(H - 240^{\circ})}{\cos(300^{\circ} - H)} \right] \quad G = \frac{1}{\sqrt{3}}(1 - S) \quad R = \sqrt{3}I - G - B \end{aligned}

彩色图像的处理范式

色彩不均衡

彩色图像常见的一种问题就是色彩不均衡，或者通俗来说，就比如说偏黄/偏绿等等，这种的常用解决方案可以采用线性变换的形式。首先我们选取一个明显的亮斑和一个明显的暗斑，按理来说，这两处的R，G，B值应该是相等的（即亮斑应该是白色，暗斑应该是黑色），但实际上往往并不是这样，因此我们可以通过线性变换来校正这些颜色。即我们可以选取一个/两个原色为基准，对另外的两个/一个原色，我们就可以通过线性变换来校正其值，使得亮斑和暗斑的三个通道值相等。假设我们选取红色为基准，那么我们可以对绿色线性变换：使 $R_{bright} = k_g(G_{bright}) + b_g$ 解出对应的k，b后再对所有像素的G值都应用对应的变换。

饱和度与色调

在RGB格式下并没有一个能直接反映饱和度和对比度的一个参数，但是在HIS格式下，就可以直观地调节饱和度，通过使S增大就可以增加饱和度，S减小就可以减小饱和度。而如果少量增加或者减少色度角，可以使颜色变得更暖/冷，但如果一次性改变色度角的幅度过大可能会导致颜色完全改变。

图像的修复

彩色图像的修复通常会在RGB格式和HIS格式中反复转换，已充分利用各自的调节优势，例如，我们可以现在RGB范围内进行线性变换平衡颜色，然后转换为HIS格式，在HIS格式中我们可以在色度和饱和度两个通道上采用中值滤波来消除背景的噪声，在消除噪声后我们可以用线性滤波来锐化图像，增强细节。而在之后我们可以对HIS的三个通道进行线性变换来保证其不偏色，最后再转换回RGB格式。

彩色图片的分割

在部分场合（例如分割文字等），基于特定通道进行分割的效果可能会非常好。

3D图像

我们生活在三维世界，传统的2D图像终究只是3D信息的某种形式的透视与投影，其会丢失维度信息，在医学图像的部分领域中这种情况更为致命，因此我们有很多办法来试图获得三维的图像。

光学切片

物理切片，产生一系列薄层切片进行成像，之后再试图重建。这是最常用也是最直观的3D成像方式。但其也有诸多问题，例如并不是所有成像对象都能切片，且切片分离后会导致配准丢失，且物理切片的过程中会产生不可避免的几何变形（拉伸卷曲等）

计算机断层扫描

最早的X光是对3D图像的直接投影，而之后提出了CT等更先进的成像方式，其通过旋转光源和探测器，以小角度步长（2-6度）记录一系列强度函数，然后将这些一维强度函数计算重建为 2D 截面图，再将截面图“堆叠”成 3D 图像，这种方式的优点是无需物理切片即可获得 3D 图像，且能较好地保留几何信息，但其缺点是辐射剂量较高，且成像时间较长。

立体测量（Stereometry）

我们单只眼睛也只能进行二维投影，能让我们有立体感是因为我们有两只眼睛，且两只眼睛的位置存在一定的距离差异，这种差异使得我们能通过视差来感知深度信息。类似地，我们也可以通过两台相机从不同角度拍摄同一场景，然后通过分析两张图像中的视差来重建场景的 3D 信息。

欲求某个平面到观测点的距离，我们通常可以采用这个公式

$R = \frac{d \sqrt{f^2 + x_l^2 + y_l^2}}{x_r - x_l}$

其中 $d$ 是两台相机的距离， $f$ 是相机的焦距， $(x_l, y_l)$ 和 $(x_r, y_r)$ 分别是左相机和右相机中某个点的坐标。即问题的核心转换为了我们如何知道同一个像素点在左右分别的位置呢。一种办法就是选定左边某个像素点及其周围信息，用一个滑动窗口遍历右边的图片，直到找到最接近的一个像素点的位置（最大化互相关/最小化差平方和）这样就能找到对应的 $x_r$ ，需要注意一般来说仅仅精确到整数像素坐标是不够的，通常需要通过插值算法算数小数点后的位移，才能得到精确的深度信息。

明暗表面显示（Shaded Surface Display，SSD）

明暗表面显示是一种基于表面渲染的三维图像显示技术，其基本思想是通过计算光线与物体表面的交点，并根据光照模型计算该点的颜色和亮度，类似于在素描等绘画中用暗部描绘阴影，用亮部来描绘反光一样，让实际上的二维图片有立体效果。其主要涉及对表面的空间描述（三角形面的拼接），对光照反射的建模，以及根据相关公式计算每处的对应灰度，一个可能的光照模型如下：

$I = A \frac{\cos(\theta)}{r^2} \frac{1}{\cos(\phi)} \{ B \cos(\phi) + (1 - B) [\cos(\theta + \phi)]^n \}$

其中I为光照强度，B，n为可调节参数，n通常代表了粗糙度，可以通过改变n来改变反射的性质（漫反射/镜面反射）

再深入可能就要进入计算机图形学的相关领域了，吓哭了。

可变形模型

最传统的图像分割就是简单的全手工人为分割，但这种方式效率极低，且分割结果也不够稳定，因此我们也想实现自动化的分割，但即使在深度学习大行其道的今天，都很难说有哪个模型能实现真正的高精确度地全自动分割，更不用提传统派图像处理算法了。因此我们设想，能不能实现一种半自动的分割办法，例如说人手动勾画一个粗糙的大致轮廓，然后由某种算法来细化。可变形模型就是基于这个思路开发的。

可变形模型将图像视为一个能量场，其中每个元素存在一个力场，这个力场会让我们手工绘制的一个粗略轮廓能被“推”到实际的边界上。

离散动态轮廓模型（Discrete Dynamic Contour）

离散动态轮廓模型是一种实现可变形模型的一种办法。为了便于理解，我们就只考虑二维结构，我们将轮廓考虑成一系列由直线相连的有序顶点，我们将顶点的坐标视为一个与变化时间/步数t相关的一个向量 $\vec{p}_i(t) = (x_i(t), y_i(t))$ 。

计算方法

基于上面我们的假设，我们将每个点视为一个可运动的点，进一步，我们假设其受力为

$\vec{f}\_i^{tot}(t) = w^{im}\vec{f}\_i^{im} + w^{in}\vec{f}\_i^{in} + \vec{f}\_i^{d}$

并且每一个点遵循运动学规则，则我们知道其会存在加速度 $\vec{a}_i(t) = \frac{1}{m}\vec{f}_i^{tot}(t)$ （通常设质量 $m=1$ ），那么我们也就知道其速度 $v_t = v_{t- \Delta t} +\Delta_t a_t$ ，更进一步有 $p_t = p_{t- \Delta t} +\Delta_t v_t$ 。

图像力

其作用是将顶点推向“能量场”的局部极小值点，而通过设计能量场的计算方式我们可以将能量场的局部极小值点定义在边缘上。例如，我们可以将能量场定义为

$E = \frac{1}{||\nabla(G\_\sigma * I)|| + \epsilon}$

其中 $G_\sigma$ 是高斯平滑，用于抗噪，而我们将图像力定义为能量场的负梯度，即：

$\vec{f}\_i^{im} = -\nabla E(x_i, y_i)$

内部力

内部力的核心目的是为了保证边缘平滑，不会因为小的噪声导致出现锯齿状的边缘，因此，内部力可以被定义为局部曲率的正比，即曲率越大（角度越尖锐），内部力越大，继而将这部分拉直，起到一个平滑边缘的作用。

（局部曲率可以被定义为两相邻顶点的所在的边向量的差值）

阻尼力 (Damping Forces)

如果没有阻尼，轮廓可能会在两个局部极小值之间震荡。阻尼力用于确保收敛。其与速度成正比，方向相反 ( $\vec{f}^d = w^d \vec{v}$ ) $w^d$ 在-1~0之间。

算法步骤

显示图像。
用户初始化轮廓（速度、加速度设为0）。
循环执行：
- 计算每个顶点的合力。
- 计算加速度。
- 更新位置和速度。
- 重采样 (Resampling) DDC。
直到所有顶点停止移动（速度和加速度小于阈值）。

重采样的必要性：随着轮廓变形，顶点之间的距离会发生变化，如果间距太大：无法紧贴弯曲的边界，如果间距太小：计算量大，浪费内存。因此，我们需要在每一步之后线性插值增加或删除顶点，使顶点间距保持均匀的距离 $\Delta$ 。

参数的影响

$\Delta$ (顶点间距)：决定了轮廓对曲线的拟合程度。 $\Delta$ 越小，拟合越精细。
$w^{in}$ $w^{in}$ (内部力权重)：控制平滑度。
- 权重低：轮廓可能由噪声引起锯齿。
- 权重高：轮廓非常平滑。
$\sigma$ $σ$ (高斯尺度)：
- 小 $\sigma$ (如2)：定位边界准确，但初始轮廓必须离边界很近。
- 大 $\sigma$ (如7)：能从更远的地方吸引轮廓（捕捉范围大），但会模糊细节，导致角点变圆。
初始轮廓：初始画的位置必须相对接近真实边界，才能被图像力“捕获”。

水平集（Level Set Method）

上述提到的DCC是一种构建可变形模型实现图形分割的办法，但其也有诸多缺点，如对本身比较凹凸不平的轮廓支持不佳（因为其算法逻辑要求其边缘需要平滑），不能同时跟踪多个物体等。而水平集是一种新的策略，其核心在于用高一维的函数曲面来表示当前的曲线，以二维边界为例，我们不将其视为一个随时间更新的边界，我们将其视为一个三维形状的在不同高度的截面，随着时间而不断上升，也不断更新，在之前可能分开的两部分可能在更高处连在一起，或是相反，这样能更自然地处理物体的合并，分裂，孔洞等复杂结构，也能简单拓展到高维，且适合并行计算。

至于具体算法太复杂了在此隐去。

不过，还是淹没了好。