形态学入门

25spring BME3304 生物医学图像处理（I）与BME4301 计算机辅助手术与治疗技术的课程笔记

形态学

基于集合论的图像处理方法, 主要用于二值和灰度图像处理.

结构元

设有两幅图像 B, A. 若 A 是被处理的对象, B 是用来处理 A 的, 则称 B 为结构元(Structuring Element, SE). 结构元可以被理解为我们所感兴趣的, 想提取的某种特征. 结构元通常比图像 A 小得多, 和滤波器比较相似. 不过结构元要更简单一点, 其就是一个二值化图像, 有三种像素(前景-1, 背景-0, 不关心-x), 在形态学运算中, 我们只关心前景像素, 因此可以把背景和不关心两种像素理解为一种.

结构元存在一个原点, 其位置可以在结构元中任意指定, 但通常位于结构元的中心位置. 结构元运算的本质就是由结构元所在的感受野中的像素值决定这个原点处的输出像素值. 对图像的遍历方式和滤波器一样, 均为滑动窗口. 不过需要注意的是滤波器可以为线性运算, 但结构元是非线性的.

形态学基本操作

基本逻辑运算

适合(fit): 感受野与结构元的前景完全重合, 需要所有的结构元前景点处像素值均为 1.
击中(hit): 感受野与结构元的前景部分重合, 只需要结构元的某一个前景点处像素值为 1 即可.

将两种基本运算运用滑动窗口应用至整张图片我们就可以得到两种基本的形态学操作: 腐蚀和膨胀

腐蚀(Erosion)

对图像每一个像素, 判断其以其为原点的感受野是否与对应的结构元完全适合, 若适合则输出像素值为 1, 否则为 0. 记作 $A \ominus B$ , 即

$A \ominus B = \{z | (B)_z \subseteq A\}$

对整个图像 $f$ 与结构元 $g$ , 则可记为

g = f \ominus s, \space g(z) = \begin{cases}1, & \text{s fits f} \\ 0, & \text{otherwise}\end{cases}

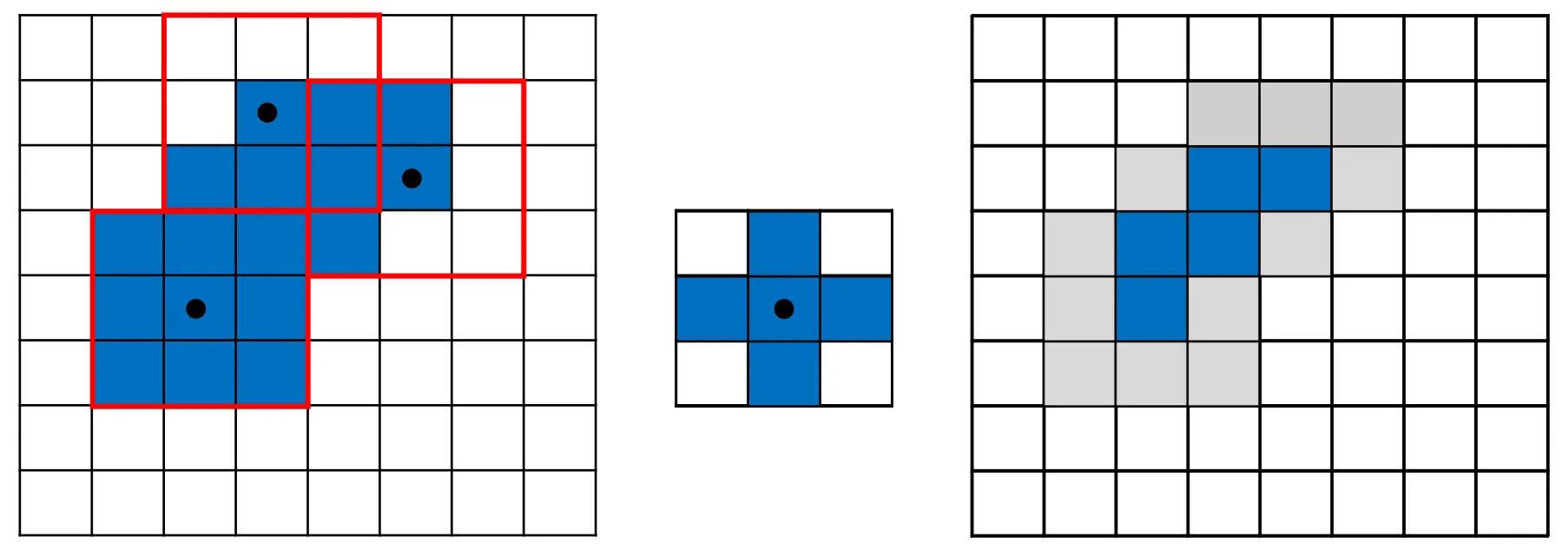
腐蚀可以用来消除边界点, 使边界向内收缩, 可以用来消除小且无意义的游离点.

膨胀(Dilation)

与腐蚀相反, 膨胀是对图像每一个像素, 判断其以其为原点的感受野是否与对应的结构元发生击中, 若击中则输出像素值为 1, 否则为 0. 记作 $A \oplus B$ , 即

g = f \oplus s, \space g(z) = \begin{cases}1, & \text{s hits f} \\ 0, & \text{otherwise}\end{cases}

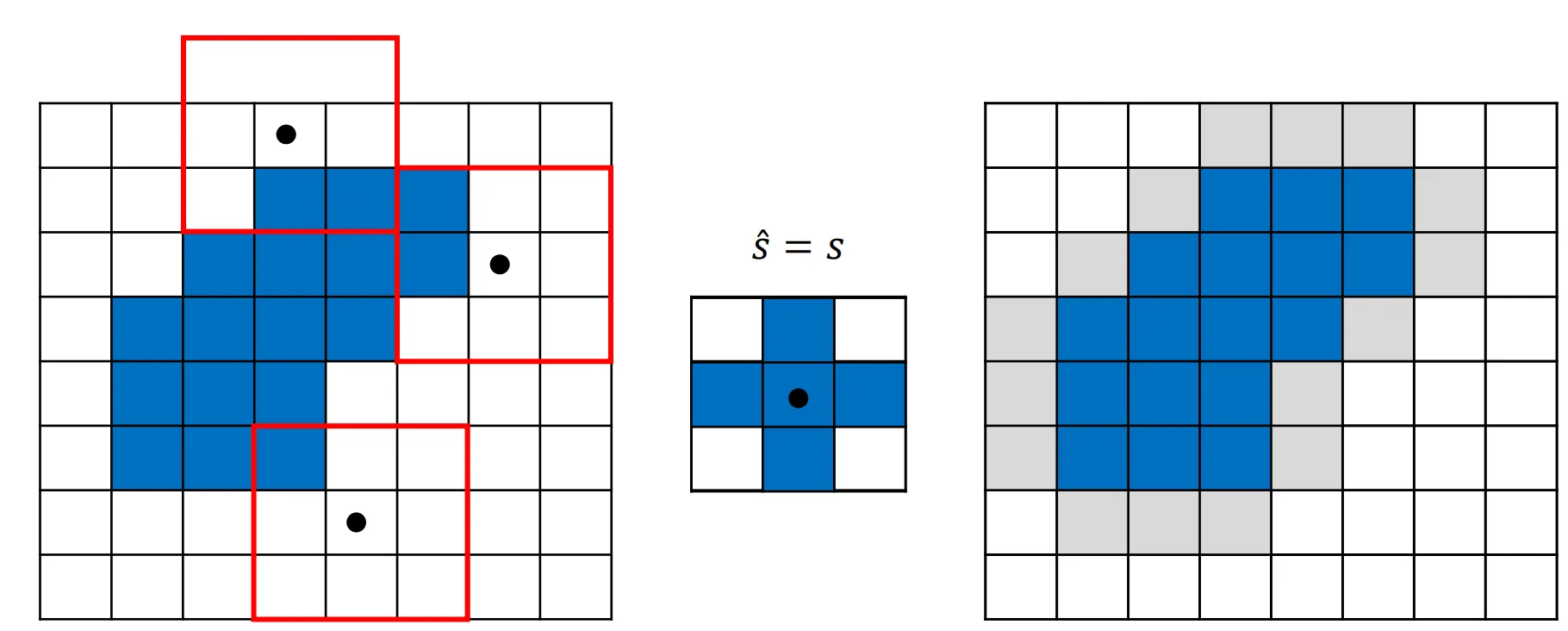
膨胀可以用来填补边界点, 使边界向外扩张, 可以用来增加物体大小, 填补缺口与凹陷.

性质与用途

腐蚀和膨胀存在对偶性

(A \ominus B)^c = A^c \oplus \hat{B} \\ (A \oplus B)^c = A^c \ominus \hat{B}

腐蚀会减小二进制对象的尺寸, 而膨胀则会增大其尺寸. 腐蚀的作用是去除孤立的小特征, 分解特征中细小的连接区域, 并通过在边界处“腐蚀”实体来减小其尺寸. 膨胀的作用大致相反, 它会加宽和加厚狭窄区域, 并使其边缘区域增大. 膨胀和腐蚀可以被理解为逆操作, 尽管它们在严格的数学意义上我们无法通过膨胀来恢复先前已被腐蚀完全去除的对象.

形态学变换

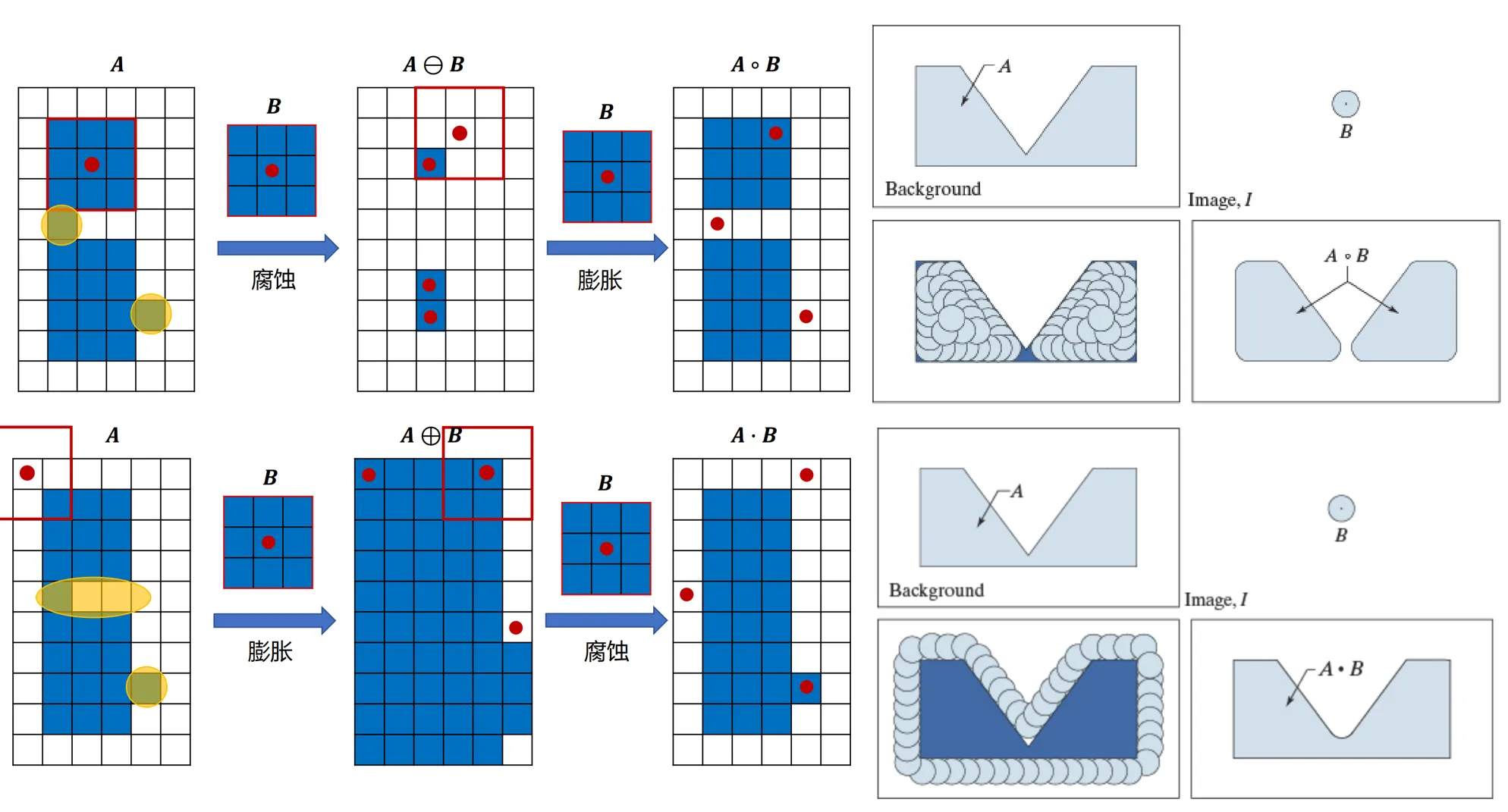
开运算(Opening)

即先对图像进行腐蚀操作, 再进行膨胀操作. 记作 $A \circ B = (A \ominus B) \oplus B$

开运算的主要作用是去除小的物体, 同时保持较大物体的形状和大小. 它可以平滑物体的边界, 断开细小的连接, 并消除噪声点. 直观上可以理解为 B 结构元在图像 A 的边界内侧“滚动”, 将 B 能达到的距原边界最远点时的结构元中心作为新的边界.

闭运算(Closing)

即先对图像进行膨胀操作, 再进行腐蚀操作. 记作 $A \bullet B = (A \oplus B) \ominus B$

闭运算的主要作用是填补小的孔洞, 同时保持较大物体的形状和大小. 它可以平滑物体的边界, 连接细小的断裂, 并消除噪声点. 直观上可以理解为 B 结构元在图像 A 的边界外侧“滚动”, 将 B 能达到的距原边界最远点时的结构元中心作为新的边界.

上: 开运算, 下: 闭运算

先进行开操作再进行闭操作是一种有效的噪声去除方法, 一方面, 开操作可以出去边缘上和游离的噪声点, 这种会导致内部的小孔洞扩大. 而这种空洞可以通过闭操作来填补.

由于开闭运算都是由腐蚀和膨胀组成, 因此它们也存在对偶性:

(A \circ B)^c = A^c \bullet \hat{B} \\ (A \bullet B)^c = A^c \circ \hat{B}

开运算与闭运算还有幂等性，即对一个图像执行1次开/闭运算与执行多次开/闭运算的结果是相同的:

击中-击不中变换(Hit-or-Miss Transform, HMT)

击中-击不中变换是一种用于检测图像中特定形状或模式的形态学操作. 它结合了腐蚀操作和结构元的概念, 通过同时考虑目标形状的前景和背景来实现对特定模式的检测. 其实本质就是腐蚀, 我们之前提到的形态学运算全部都是只考虑前景, 不考虑背景, 那么 HMT 其实就是对前景和背景都进行形态学操作而已(具体而言就是把像素翻转, 然后再进行一次腐蚀操作), HMT 被记作 $\circledast$

形态学算法基础

边界提取

边界提取的方式就是首先使用一个全为前景像素的结构元腐蚀 A, 再用 A 减去腐蚀后的结果(求差集), 可记为:

$\beta(A) = A - (A \ominus B)$

基于形态学的边界提取方法有效克服了空间滤波定位精度较差, 对噪声敏感, 准确性不高的缺点, 而且避免了检测出来的边缘通常是不连续和不规则的.

孔洞填充

孔洞填充的基本思想是从孔洞内的某个种子点开始, 通过膨胀操作逐步扩展, 直到填满整个孔洞为止. 公式可以记为:

$X_k = (X_{k-1} \oplus B) \cap A^c \\ \text{stops when }X_k = X_{k-1}$

这里最初的的 $X_{k0}$ 是空洞内的一个"种子点", 是事先将空洞中的一个点翻转为前景时得到的. 这里使用的结构元 $B$ 是一个十字形(四连通)结构元.(四连通的好处是膨胀相对比较稳定, 如果使用八连通可能会在拐角处出现膨胀溢出的情况)

对这个算法的一种理解, $(X_{k-1} \oplus B) \cap A^c$ 本质是一个不断膨胀的过程, 这也是我们所需要的, 而我们需要控制其膨胀的边界, 这里的边界也就是空洞的边界, 也就是如果膨胀到了原图像的前景区域就停止, 因此我们用与运算和 $A^c$ 来控制边界, 直到膨胀不再变化为止.

注: 一次性找到所有空洞的一种巧思: 将所有孔洞视作与边界没有直接连通的部分, 因此我们选择一个边界像素作为种子, 将孔洞的边界作为限制进行膨胀, 膨胀到最后始终无法被覆盖的部分就是孔洞部分.

连通分量的提取

连通分量的提取其实与空洞填充是类似的, 只是这里我们是从一个前景点开始膨胀, 以及与之前的情况不同, 因为我们需要保证膨胀结果完全覆盖连通前景, 所以一般采用的是八连通结构元. 公式可以记为:

$X_k = (X_{k-1} \oplus B) \cap A \\ \text{stops when }X_k = X_{k-1}$

形态学中的形态

凸壳

凸壳(Convex Hull)是指包含图像中所有前景像素的最小凸多边形, 从定义上来看, 如果一个集合中任意两点之间的连线都完全包含在该集合内, 则该集合是凸的.

在形态学中, 寻找一个可以包含某一形状的凸壳可以通过一系列的击中-击不中变换来实现, 具体可以定义四个结构元:

B_1 = \begin{bmatrix} 1 & \times & \times \\ 1 & 0 & \times \\ 1 & \times & \times \end{bmatrix}, \quad B_2 = \begin{bmatrix} 1 & 1 & 1 \\ \times & 0 & \times \\ \times & \times & \times \end{bmatrix}, \quad B_3 = \begin{bmatrix} \times & \times & 1 \\ \times & 0 & 1 \\ \times & \times & 1 \end{bmatrix}, \quad B_4 = \begin{bmatrix} \times & \times & \times \\ \times & 0 & \times \\ 1 & 1 & 1 \end{bmatrix}

然后我们分别用这些结构元对图像 A 进行击中-击不中变换, 直到一次变换后图形不变化为止, 公式可以记为:

$X_k = (X_{k-1} \circledast B_i) \cup X_{k-1}, \\ \text{stops when }X_k = X_{k-1}, \text{ let } D^i = X_k^i, \\ \text{A convex hull of A is } C(A) = \bigcup_i^4 D^i.$

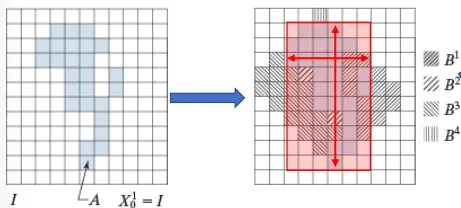
我们可以将这种求凸壳的方式理解为一个像素一个像素地“填充”图像的凸包, 通过不断地对图像进行击中-击不中变换, 将图像中的凹陷部分逐步填平, 最终形成一个凸壳. 值得一提的是, 这里得到的凸壳无法保证是最小尺寸的凸壳(例如上图中阴影是通过形态学求得的凸壳, 而红色矩阵为理论最小凸壳)

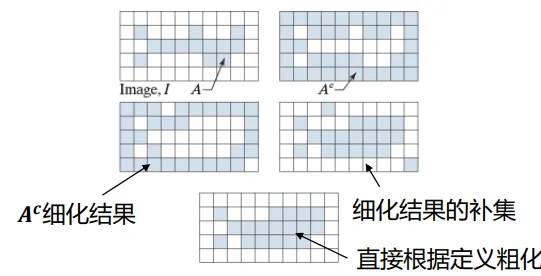
细化

细化(Thinning)是一种形态学操作, 其目的是将二值图像中的前景对象逐步“削薄”. 细化操作通常用于图像分析和模式识别, 因为它可以保留对象的拓扑结构和几何特征, 同时减少数据量, 基于 HMT 的细化计算可记为:

$A \otimes B = A - (A \circledast B) = A \cap (A \circledast B)^c$

为保证效果, 一般我们会采取不止一个结构元进行细化操作, 常见的有八个结构元, 分别对应八个方向(上下左右及四个对角线方向), 一个常见的结构元序列为:

B_1 = \begin{bmatrix} 0 & 0 & 0 \\ \times & 1 & \times \\ 1 & 1 & 1 \end{bmatrix}, \quad B_2 = \begin{bmatrix} \times & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & \times \end{bmatrix}, \quad B_3 = \begin{bmatrix} 1 & \times & 0 \\ 1 & 1 & 0 \\ 1 & \times & 0 \end{bmatrix}, \quad B_4 = \begin{bmatrix} 1 & 1 & \times \\ 1 & 1 & 0 \\ \times & 0 & 0 \end{bmatrix},

B_5 = \begin{bmatrix} 1 & 1 & 1 \\ \times & 1 & \times \\ 0 & 0 & 0 \end{bmatrix}, \quad B_6 = \begin{bmatrix} \times & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & \times \end{bmatrix}, \quad B_7 = \begin{bmatrix} 0 & \times & 1 \\ 0 & 1 & 1 \\ 0 & \times & 1 \end{bmatrix}, \quad B_8 = \begin{bmatrix} 0 & 0 & \times \\ 0 & 1 & 1 \\ \times & 1 & 1 \end{bmatrix},

每个结构元是前一个结构元顺时针旋转 45°(看不出来怎么转的? 看 $\times$ 像素位置即可), 依次使用这些结构元进行细化即可得到最终结果. (如果一轮得不到结果就再来一轮)

粗化

粗化是细化的对偶过程, 使用单个结构元的粗化可以定义为:

$A \odot B = A \cup (A \circledast B)$

定义一个形态化序列 $B = \{B^1, B^2, \ldots, B^n\}$ 使用结构元序列进行粗化可定义为:

$A \odot B = ((\ldots((A\odot B^1) \odot B^2) \odot \ldots) \odot B^n)$

但是实际上, 粗化通常通过前景/背景反转后细化再翻转得到.

模式谱（Pattern Spectrum）[only in BME4301]

类似于灰度直方图，模式谱旨在统计一个图片中不同尺寸物体的数量与占比。直观地说，就是用逐渐增大的结构元对图像进行开运算，如果一个元素被某个大小的结构元去掉了，就说明他大概就属于这个结构元所在的尺寸（或者说小一点）。而从整个图来看，通过统计每次开运算前后图像中前景像素的数量变化，我们就可以得到一个关于图像中不同尺寸物体分布的统计信息，这个信息就被称为模式谱。从数学上定义，模式谱可以表示为：

PS_{r_iK}(F) = Card((F \circ S_{r_iK}) - (F \circ S_{r_{i+1}K}))

(Card在此处即指像素的个数/形状的面积)

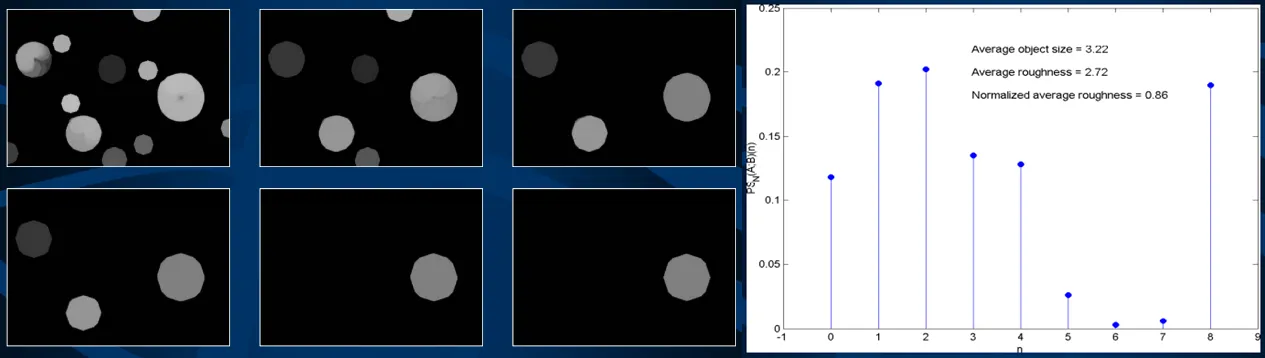
模式谱的一个重要应用是纹理分析与分类。不同纹理通常由不同尺寸和形状的基本单元组成，通过分析模式谱，我们可以提取出这些基本单元的尺寸分布特征，从而实现对纹理的识别与分类。

但值得注意的是，模式谱只能反应图片中某个纹理的尺寸大小，并不能反应其所处位置。

递归/连续腐蚀（Recursive Erosion）[only in BME4301]

用一个小的腐蚀操作连续腐蚀多次，形成类似等高线的处理流程。常用于距离变换，骨架提取，分割等。

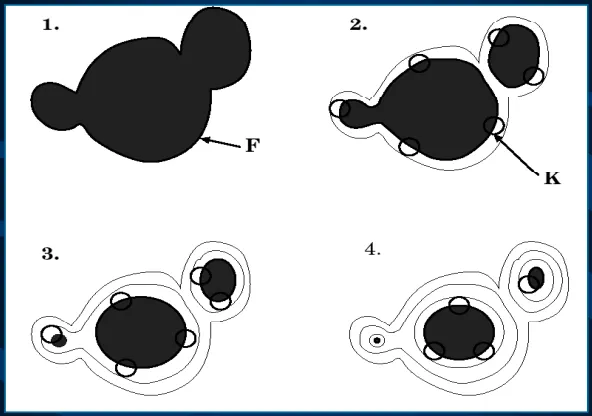
距离变换（Distance Transform）[only in BME4301]

距离变换只用于二值化图像，其用法是对图片进行多次连续腐蚀直到图片完全被腐蚀，每个像素在消失前被腐蚀的次数就是该像素到最近边界的距离。

距离变换一般有三种，欧几里得距离 $D_{Euclid} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$ ，使用方形结构元得到的距离即为欧几里得距离。城市街区距离 $D_{city} = |x_2 - x_1| + |y_2 - y_1|$ ，使用十字形结构元得到的距离即为城市街区距离。棋盘距离 $D_{chessboard} = \max(|x_2 - x_1|, |y_2 - y_1|)$ ，使用圆形结构元得到的距离即为棋盘距离。

骨架的提取与重建 [only in BME4301]

骨架保留了原有的拓扑结构，但其处处之只有1像素宽。需要注意的是其不是距离变换中全局最大值部分的集合，其是局部（4/8领域）最大值的像素的集合。其处理方式类似所谓“草原大火”，假设前景为草地，火从边缘开始燃烧，若火相遇则停止燃烧，最终剩下的未燃烧部分即为骨架。其是所有双切线圆的圆心的集合。

提取算法

设原图像为 $Img$ ，结构元为 $K$ （K通常为3x3方形或十字星结构元），则骨架的提取步骤为：

对当前图片进行腐蚀，得到 $Eroded = Img \ominus K$
对腐蚀后的图片进行开运算，得到 $Opened = Eroded \circ K$
得到当前的骨架子集 $Subset = Eroded - Opened$ （这一步的逻辑是我们知道开运算是为了去除毛刺，而实际上这些毛刺就是物体的中心骨架点）
将得到的骨架子集加入骨架图像中（list.append, 或者取并集） $Skeleton = Skeleton \cup Subset$
若 $Eroded$ 不为空，重复步骤1-4，否则结束。

重建算法

如果单纯用最后的骨架结果肯定不能完美重建，如果需要完美重建需要保留每步时得到的骨架子集。或者另一种办法，需要有原图的距离变换，在重建时按照骨架点处的距离值来选择膨胀的结构元。

重建公式：

$F = \bigcup_{i=0}^{n} (S_i(F) \oplus r_i K)$

对骨架进行有针对性的重建（例如只重建骨架中距离值大的部分）可以消除毛刺，而对大部分情况而言，存储骨架+距离是无损的更省存储空间的一种储存方式。

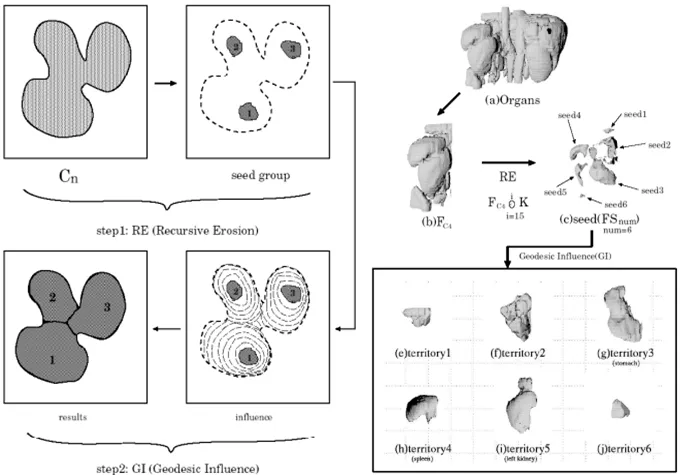
极限腐蚀与条件膨胀（Ultimate Erosion & Geodesic Influence）[only in BME4301]

本质上是距离变换的一种拓展形式，不是单纯求整个图形的距离，其会监测递归腐蚀过程中的联通量的变化，将一个粘连的物体腐蚀成互不相连的多个种子点，而每个像素的居里点是从其所属联通量与其他联通量分开始开始计算，最终生长出多个互不侵犯的区域。

灰度级形态学

腐蚀与膨胀

灰度级腐蚀和膨胀是形态学操作在灰度图像上的扩展. 让我想起了池化层里的 min/max pooling 的逻辑.

灰度级形态学中的结构元分为不平坦结构元和平坦结构元,结构元包含两个参数, 形状和灰度值(高度, 或者说偏置), 平坦结构元的偏置灰度值全部相同(可以理解为 0), 而不平坦结构元的不同位置偏置灰度值不同. 在灰度学形态学中, 结构元 $b$ 对图像 $f$ 的腐蚀与膨胀可以分别定义为:

[f \ominus b_N ](x, y) = \min_{(s, t) \in b_N} \{f(x+s, y+t) - b_N(s, t)\} \\ [f \oplus b_N ](x, y) = \max_{(s, t) \in b_N} \{f(x-s, y-t) + \hat{b_N}(s, t)\} \\ (b_N \equiv const \text{ if SE is flat}) \\

其中 $b_N$ 表示结构元的前景部分, $\hat{b_N}$ 表示结构元的中心翻转. 而且注意腐蚀是 f(x+s, y+t), 而膨胀是 f(x-s, y-t), 哎呀好复杂好复杂, 不过鉴于结构元大部分都是中心对称的, 所以可以不管这个翻转和加减的问题.

我们通常认为腐蚀后的灰度图像要比原图像暗，即暗特征变大，亮特征变小.

而膨胀的效果为亮特征变大，而暗特征变小.

（我觉得这个图挺直观的，上为膨胀，下为腐蚀）

开运算与闭运算

与二值形态学类似, 灰度形态学中的开运算和闭运算也是由腐蚀和膨胀组成的复合操作. 灰度形态学中的开运算和闭运算可以分别定义为:

f \circ b_N = (f \ominus b_N) \oplus b_N \\ f \bullet b_N = (f \oplus b_N) \ominus b_N

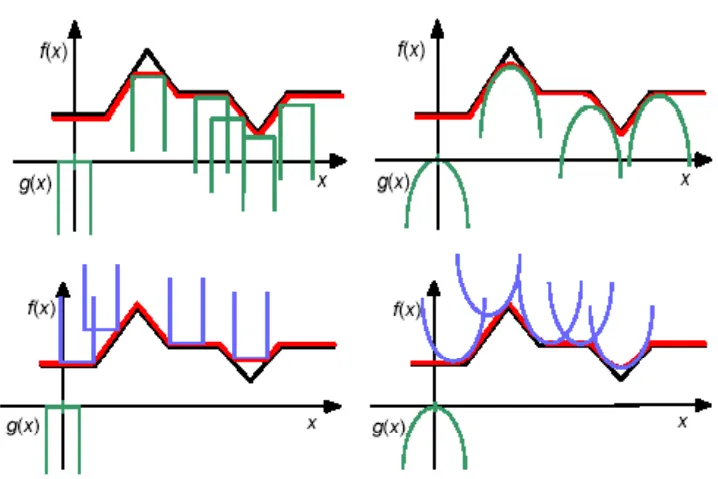
开运算对图像中暗特征和背景的影响可以忽略不计，但亮特征变小，变小的程度取决于这些特征相对于结构元大小(压制亮特征),

闭运算对图像中亮特征和背景的影响可以忽略不计，但暗特征变小，变小程度取决于这些特征相对于结构元大小(压制暗特征).

腐蚀膨胀与开运算闭运算都有对偶性, 与二值形态学类似.

形态学梯度

灰度图像 $f$ 对结构元 $b$ 的形态学梯度可以定义为:

MG(f) = (f \oplus b) - (f \ominus b)

b 通常用 3x3 元素的平坦结构元, 其可以产生类似于梯度的效果, 有描绘区域边界的作用。更具体地说，我们还可以将边界分为外边界和内边界，这样还可以定有外梯度 $Gradient(F)_E = \frac{1}{2}(f \oplus b - f)$ 和内梯度 $Gradient(F)_I = \frac{1}{2}(f - f \ominus b)$ 。

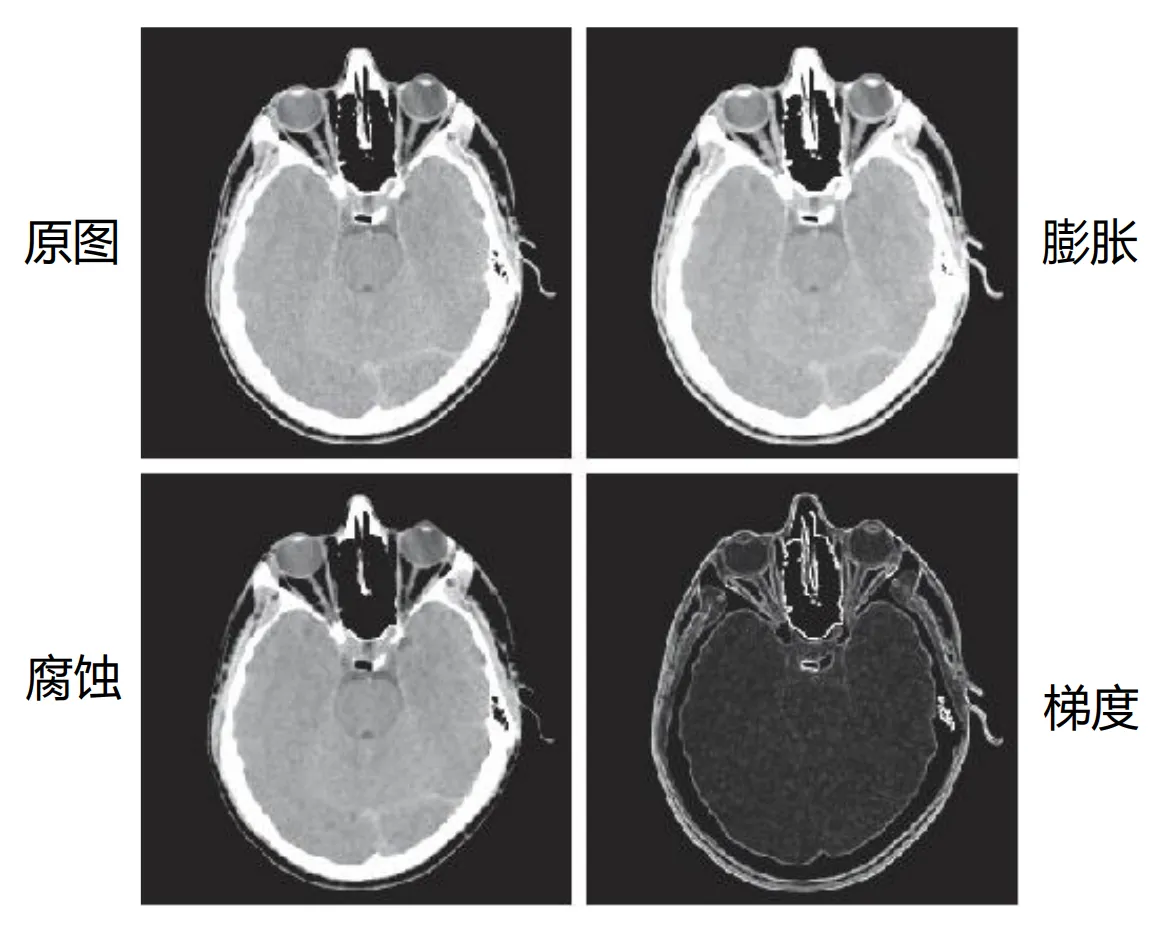
注：BME4301的课件里面梯度要乘一个1/2

常用算法

平滑与去噪

平滑滤波器可以通过开运算和闭运算来实现. 开运算可以去除图像中的小亮点噪声, 而闭运算可以去除小暗点噪声. 通过先进行开运算再进行闭运算, 是一般情况下最有效的去噪方法.

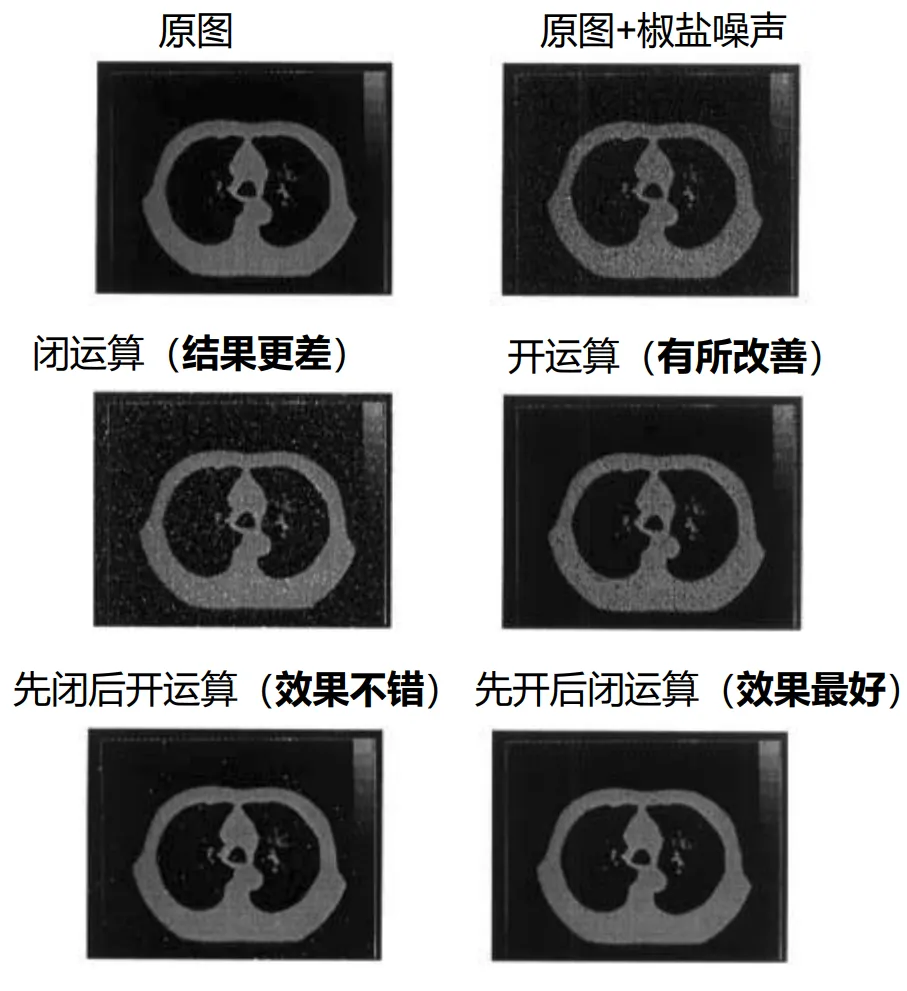
除此之外还有一种平滑方式 DSmooth （Dynamic Smooth），公式为

DSmooth(f) = \frac{1}{2} [(F \oplus b) + (F \ominus b)]

顶帽变换与底帽变换 (Top-hat & Bottom-hat)

白顶帽变换: $T_{hat}(f) = f - (f \circ b_N)$
黑底帽变换: $B_{hat}(f) = (f \bullet b_N) - f$

顶帽变换的一个重要作用时矫正如光照不均衡导致的背景颜色对识别前景要素的影响.

差分顶帽变换（Differential Top-hat Transform） [only in BME4301]

传统的顶帽变换存在的问题是, 其结果依赖于所选结构元的大小。于是我们自然而然地想到，利用一系列的结构元去做顶帽变换。但这又带来了一个问题，那我们该如何决定这个这一系列的顶帽变换的结果该保留哪些，舍去哪些，又该如何合并呢。差分顶帽变换就提供了一种解决方案。其会利用一系列大小递增的结构元去做顶帽变换，然后计算相邻两次顶帽变换结果的差分，对每一个差分结果，我们对其进行一次自定义阈值的阈值变换，保留大于阈值的部分，舍去小于阈值的部分。最后将所有保留下来的部分进行合并，得到最终结果。数学公式可以表示为

F_i = |T_i - T_{i-1}|_B - F'_{i-1} \text{ where, } F'_i = \bigcup_{1 \le j \le i} F_j; F'_1 = \emptyset

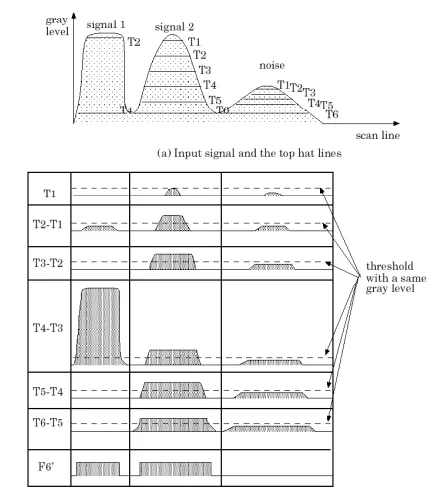
如图所示，这种办法可以神奇地抹除一些背景噪音，说不定在某些场合上会有奇效

fun fact：这几张杂志封面（据gemini称）发布时间约为20世纪90年代中期

粒度测定

粒度测定的根据是: 不同大小的结构元会对图像中的不同大小的颗粒产生不同的影响. 通过对图像进行一系列不同大小结构元的开运算, 可以分析图像中不同大小颗粒的分布情况.

（好像这个的二值化形式就是上文提到的模式谱？）

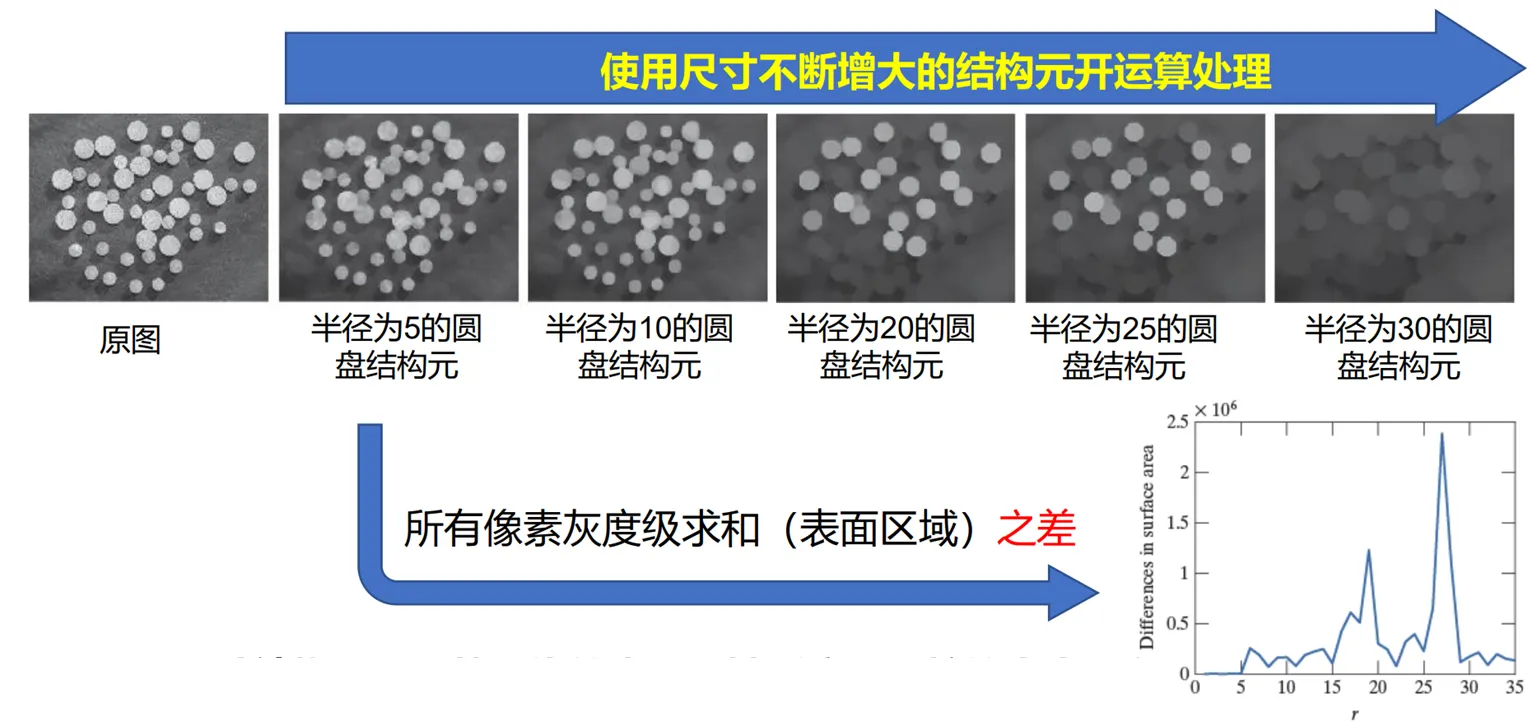
纹理分割

例如, 下面最左边这个图像, 显然我们可以"感觉"出来这里面的点分为了左半片比较小的, 和右半片比较大的. 但我们如何该从算法层面来实现呢. 我们可以首先选一个大小在小点与大点之间的结构元, 然后对图像进行开运算, 这样左半部分的小点就会被抹掉, 而右半部分的大点则会被保留. 这样我们只留下了右边的大点, 而我们再通过闭运算, 将右边分别独立的大点连成一个整体, 然后我们可以通过形态学或者其他方法得到两区域之间的边界.

条件膨胀 [only in BME4301]

其有两个输入图像，marker和mask，对于二值化图片来看，我们可以就直接在二维平面上考虑，marker图像可以被理解为种子，而mask图像可以被理解为其被限制的生长的区域，或者可以理解为土壤。对于灰度值的话还要考虑其每个像素位点上的灰度值不能超过mask对应位点的灰度值。

其数学定义为：

R_i(M,V) = (M \overset{i}{\oplus} K) \cap V, \text{ until } R_i(M,V) = R_{i-1}(M,V)

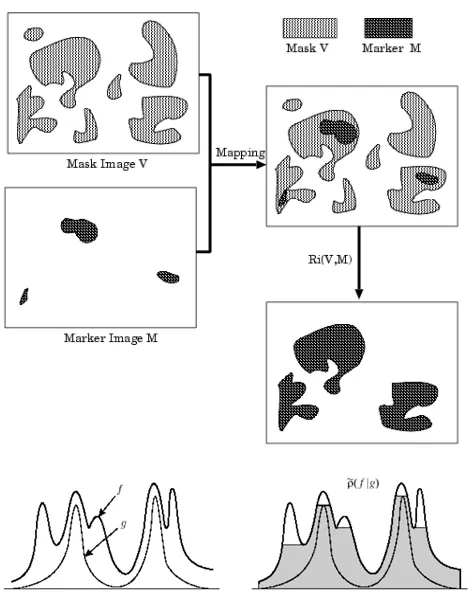
灰度重建 [only in BME4301]

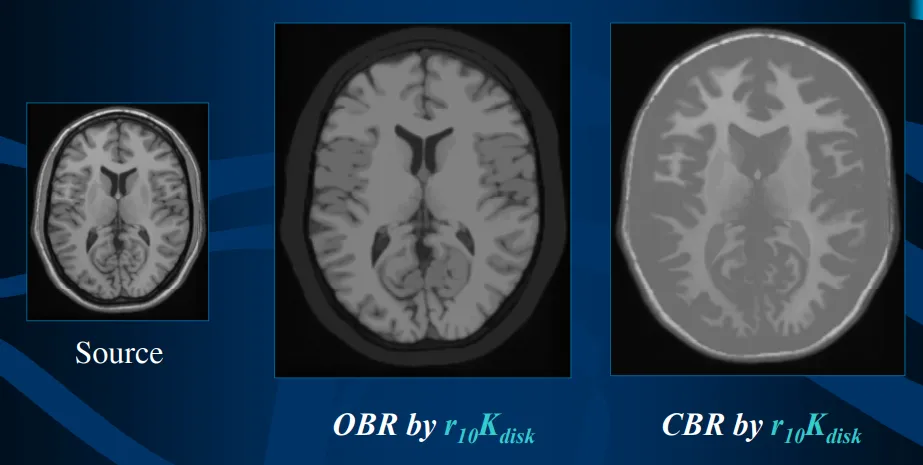
基于重建的开运算（OBR）：先进行开运算，然后进行条件膨胀，可以去除亮的小物体/噪声，同时保留较大物体的完整边缘形状

基于重建的闭运算（CBR）：先进行闭运算，然后进行条件腐蚀，可以填补暗的孔洞/斑点，同时保留整体形状

形态学

结构元