Machine Learning Notes 2

一些优化方法

momentum

python

optimizer = torch.optim.SGD(model.parameters(), lr=config['learning_rate'], momentum=0.9)

momentum在物理上即为动量，以我大物一期末卷面56分的物理水平去理解，感觉其理念和“惯性”也很相似原来的的梯度下降“下降距离“仅取决于梯度和Learning rate。可以知道在梯度为0的时候就会自动停止了。因此，优化时很有可能卡在一个局部极小值，而非全局最小值。以最简单的二元函数为例，我们可以想象原来的梯度下降法就是一个球在一个崎岖不平的坡随机从一点不断往下滑，这样可能的问题我们有一定概率滑到一个局部最小值，而非全局最小值就停止了。加入了momentum之后，这个球有了一定的惯性/动量，即使在梯度为0的局部最小值也会继续沿着原来前进的方向再滚动一段距离，也就有可能滚出这个局部最小值的区域。对于更多参数虽然难以想象，但大概同理。

正则化

众所周知过拟合是一个严重而常见的方法，解决它的一种策略就是采用正则化。如下图，蓝色区域即为缺失函数的图像（本图中假设中间为极小值点），我们可以预设在靠近极小值的时候会出现过拟合情况，于是我们某些方法限制了可能的未知数取值（即途中的橙色区域），~~其实就是条件极值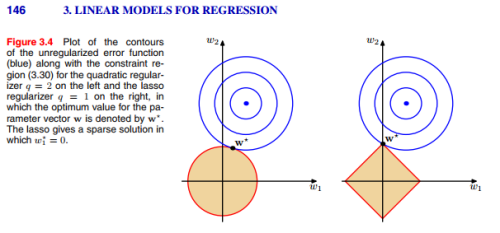~~ 图中第一个图为L1正则化，第二个图为L2正则化。在pytorch中的最简单的一种实现方法就是增加一个weight_dacay参数。

python

optimizer = torch.optim.SGD(model.parameters(), lr=config['learning_rate'], momentum=0.9,weight_decay=0.0001)

Adam

除了momentum的引入之外，另一种改进的方向是调整learning rate，较早的尝试即为RMSProp，这种优化算法主要基于梯度的方差（二阶矩）来调整learning rate。在这之后有人将RMSProp与momentum的理念结合在了一起，设计了Adam（Adaptive Moment Estimation）。Adam是当今很多主流模型采用的优化法。基于Adam优化改进的优化算法和基于SGD衍生的算法有很多，形成了两大大类，其中，基于Adam的算法速度更快，但可能有不稳定，在测试集中表现较差的情况。相比之下，SGD系的准确率更高，但相对来说训练时间较长，如今也有试图集二者之长的优化算法出现，如SWATS等。

lookahead

Lookahead是被提出来的一种改进优化器表现的策略，其一般和别的优化器（SGD，Adam）之类的结合使用，其理念则是不会直接算一次梯度就前进一次，其会先多算几次模拟下降情况（Fast weights），但最后模型参数的正式更新会根据这几次的最终结果来判断实际的方向和下降程度（Slow weights）

scheduler

除了本身在optimizer中自动规定的learning rate以外，你也可以用scheduler对learning rate进行更改，常见的scheduler如余弦退火（Cosine Annealing）其是一种学习率调度策略，它根据余弦函数的周期性变化来调整学习率。这种策略模仿了金属退火的过程，通过逐渐降低温度来使金属达到一种稳定的状态。在机器学习中，余弦退火用于使学习率随时间逐渐减小，从而帮助模型更好地收敛。 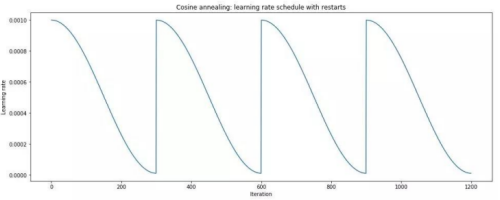scheduler一般一次epoch更新一次，简单实现方式如下

text

# 假设已经定义了optimizer和模型等
scheduler = CosineAnnealingLR(optimizer, T_max=10)

for epoch in range(num_epochs):
    ###########
    # 训练模型 #
    ###########
    scheduler.step()

ReLU激活函数以及其改进

ReLU函数，即Rectified Linear Unit，是在深度学习广泛运用的激活函数，其表达式非常简单 [ \text{ReLU}(x)=\max(x) ] 显而易见这个函数有诸多好处，其在非负数部分为线性，非常好计算，同时也避免了其他部分激活函数（如sigmoid函数）在部分函数段的梯度趋近与0导致最终权重变化极慢甚至停滞的问题。当然普通的ReLU也有不足之处，例如若在其输入为负数时，同样会出现梯度为0的情况，称为dead ReLU。当然这个解决办法非常简单，就是修改一下负数部分的表示，因此就有了LeakyReLU和ELU等ReLU改进版。 [\text{LeakyReLU} (x)=\max (\alpha x,x)]
[\text{ELU} (x)= \max (0,x)+\min(0,\alpha(\exp(x)-1))]
上述二者也均在pytorch中可以直接调用

python

nn.LeakyReLU(0.1)
nn.ELU(0.1)
#可选参数均为alpha值

network structure tricks

residual network

残差网络旨在让网络学习输入输出之前的差异，而非输出本身，这种策略可以有效规避在深层网络中可能出现的梯度消失的问题。其代码实现可以很简单，最简单的代码实现只需要在每一层输出之后再加上这一层的输入即可。 Kaiming He数年前基于此理论提出的ResNet，成为了深层神经网络发展的重要里程碑。

spatial transformer networks

在训练卷积神经网络用于图像处理时，我们不难发现CNN其实并不能“理解“平移，旋转，缩放等概念。一方面我们可以通过对输入的图像进行图像变换来让CNN强行把所有的情况都学到，另一种方法我们同样可以使用Spatial Transformer Networks（ST）来还原这种变换。ST可以是穿插在卷积层之间的神经层。从数学的角度来看，图像的平移，旋转，放大等的微观层面则是图片每个像素都发生了转移，而所有像素的转移都可以用某个矩阵来表示，因此ST的本质也就是来求解这个这个矩阵。下面就是一个简单的求解仿射变换（假设有6个参数）的ST网络

python

import torch
import torch.nn as nn
import torch.nn.functional as F

class ST(nn.Module):
    def __init__(self, num_features):
        super(ST, self).__init__()
        # 假设输入特征图有 num_features 个通道
        self.fc = nn.Linear(num_features, 6)  # 学习仿射变换的6个参数

    def forward(self, x):
        # x 是输入特征图
        theta = self.fc(x.view(x.size(0), -1))  # 展平特征图并预测变换参数
        theta = theta.view(-1, 2, 3)  # 重排参数为仿射矩阵

        # 生成网格并应用变换
        grid = F.affine_grid(theta, x.size())
        x_transformed = F.grid_sample(x, grid)  # 变换特征图
        return x_transformed

Reference

李宏毅机器学习